
����Ŀ����ͼ��![]() �Ƕ�������Ĺ�·����ı�Ե�ߣ�ij��˾����
�Ƕ�������Ĺ�·����ı�Ե�ߣ�ij��˾����![]() �ϵ�һ��
�ϵ�һ��![]() �����������
�����������![]() ������һ�ֿ⣬��
������һ�ֿ⣬��![]() �����ڹ�·���ཨ��߳�Ϊ
�����ڹ�·���ཨ��߳�Ϊ![]() ������������תվ
������������תվ![]() ������
������![]() ��
��![]() �ϣ����ִӲֿ�
�ϣ����ִӲֿ�![]() ��
��![]() ����תվ�ֱ���������·
����תվ�ֱ���������·![]() ����֪
����֪![]() ����
����![]() ��
��

��1����![]() ����
����![]() �ĺ�������ʽ�������������
�ĺ�������ʽ�������������
��2�������תվ�Ķ�Χǽ���Ϊ10��Ԫ![]() ��������·���Ϊ30��Ԫ
��������·���Ϊ30��Ԫ![]() ���ʣ�
���ʣ�![]() ȡ��ֵʱ���ù�˾������תվΧǽ��������·�����
ȡ��ֵʱ���ù�˾������תվΧǽ��������·�����![]() ��ͣ�
��ͣ�
���𰸡���1��![]() ����2��
����2��![]() .
.
��������
��1���ڡ�BCF�У�CF=x����FBC=30�㣬CF��BF��BC=2x���ڡ�ABC�У�AB=y��AC=y-1����ABC=60�㣬�����Ҷ�������⺯���Ľ���ʽ��Ȼ����ⶨ����2�����M=30��2y-1��+40x��ͨ����������ʽ������ʽ����ֵ���ɣ�
��1���ڡ�BCF�У�CF��x����FBC��30�㣬CF��BF������BC��2x��
�ڡ�ABC�У�AB��y��AC��y��1����ABC��60�㣬
�����Ҷ�������AC2��BA2+BC2��2BABCcos��ABC��
�� ��y��1��2��y2+��2x��2��2y2xcos60�㣬
���� ![]() ��
��
��AB��AC��BC����![]() ������Ϊ
������Ϊ![]() ��0������x��1��
��0������x��1��
���Ժ���![]() �Ķ������ǣ�1��+�ޣ���
�Ķ������ǣ�1��+�ޣ���
��2��M��30��2y��1��+40x��
��Ϊ![]() ����x��1��������M��30
����x��1��������M��30![]()
�� M��10![]() ��
��
��t��x��1����t��0������M��t����10��16t+![]() ����t��0���ɻ�������ʽ��M��t����10��2
����t��0���ɻ�������ʽ��M��t����10��2![]() ����490��
����490��
���ҽ���t��![]() ����x��
����x��![]() ʱȡ�Ⱥţ�
ʱȡ�Ⱥţ�
�𣺵�x��![]() kmʱ����˾����תվΧǽ��������·��������MΪ490��Ԫ��
kmʱ����˾����תվΧǽ��������·��������MΪ490��Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
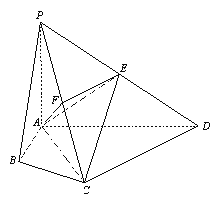
����Ŀ��(14��)������P��ABCD�У���ABC����ACD��90������BAC����CAD��60����PA��ƽ��ABCD��EΪPD���е㣬PA��2AB��2��
������������P��ABCD�����V��
��������FΪPC���е㣬��֤PC��ƽ��AEF��
��������֤CE��ƽ��PAB��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ֱ������![]() �У�AB��CD��
��AB��CD��![]() ����
����![]() ������
������![]() Ϊһ������������������
Ϊһ������������������![]() ��Ȼ���ر�
��Ȼ���ر�![]() ��������
��������![]() ���ۣ�ʹƽ��
���ۣ�ʹƽ��![]() ��ƽ��
��ƽ��![]() ��ֱ����ͼ2��
��ֱ����ͼ2��


������֤��BC��ƽ��DBE��
�������D��ƽ��BEC�ľ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����A��0��2����ֱ��![]() ����ԲC��
����ԲC��![]() ����P��Q���㣮
����P��Q���㣮
��1����ֱ��![]() ��б��Ϊk����k��ȡֵ��Χ��
��б��Ϊk����k��ȡֵ��Χ��
��2������PQΪֱ����Բ������E��1��0������ֱ��![]() �ķ��̣�
�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ϵ�ļ�����ֱ������ϵ��ԭ���غϣ�������ֱ������ϵ��x����������غϣ�������C�IJ�������Ϊ ![]() �����Dz�������ֱ��l�ļ����귽��Ϊ
�����Dz�������ֱ��l�ļ����귽��Ϊ ![]() ��sin���ȩ�
��sin���ȩ� ![]() ��=1��
��=1��
��1��������C�IJ������̻�Ϊ�����귽�̣�
��2����ֱ��l��һ��������C�����ߣ������߳�����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ������£��������ɵ��ϵij����ٶ� ![]() ����λ��ǧ��/Сʱ���dz����ܶ�
����λ��ǧ��/Сʱ���dz����ܶ� ![]() ����λ����/ǧ�ף��ĺ����������ɵ��ϵij����ܶȴﵽ200��/ǧ��ʱ����ɶ�������ʱ�����ٶ�Ϊ0ǧ��/Сʱ���������ܶȲ�����20��/ǧ��ʱ�������ٶ�Ϊ60ǧ��/Сʱ���о���������
����λ����/ǧ�ף��ĺ����������ɵ��ϵij����ܶȴﵽ200��/ǧ��ʱ����ɶ�������ʱ�����ٶ�Ϊ0ǧ��/Сʱ���������ܶȲ�����20��/ǧ��ʱ�������ٶ�Ϊ60ǧ��/Сʱ���о��������� ![]() ʱ�������ٶ�
ʱ�������ٶ� ![]() �dz����ܶ�
�dz����ܶ� ![]() ��һ�κ�����
��һ�κ�����
��1���� ![]() ʱ������
ʱ������ ![]() �ı���ʽ��
�ı���ʽ��
��2���������ܶ�Ϊ���ʱ������������λʱ����ͨ�����ɵ���ij�۲��ij���������λ����/Сʱ�� ![]() ���Դﵽ���������ֵ������ȷ��1��/Сʱ��
���Դﵽ���������ֵ������ȷ��1��/Сʱ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ȱ�����{an}�У���������am��anʹ��![]() =4a1 �� ��a6=a5+2a4 �� ��
=4a1 �� ��a6=a5+2a4 �� ��![]() ����Сֵ�ǣ�������
����Сֵ�ǣ�������
A.![]()
B.2
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������� ![]() ��ͼ������ƽ��m��m��0������λ���Ⱥ����õ���ͼ�����y��Գƣ���m����Сֵ�ǣ� ��
��ͼ������ƽ��m��m��0������λ���Ⱥ����õ���ͼ�����y��Գƣ���m����Сֵ�ǣ� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��3������F��x��=min{2|x��1|��x2��2ax+4a��2}������min��p��q��= ![]()
��1����ʹ�õ�ʽF��x��=x2��2ax+4a��2������x��ȡֵ��Χ
��2����1����F��x������Сֵm��a��
��3����F��x����[0��6]�ϵ����ֵM��a��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com