
已知 .
.
(1)若 恒成立,求
恒成立,求 的最大值;
的最大值;
(2)若 为常数,且
为常数,且 ,记
,记 ,求
,求 的最小值.
的最小值.
(1)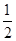 ;(2)
;(2)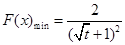 .
.
解析试题分析:本题考查导数与函数及运用导数求单调区间、最值等数学知识,突出考查运用数学知识和方法分析问题解决问题的能力.第一问,是恒成立问题,先将恒成立问题转化为最值问题,求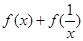 的最值是本问的关键,法一,利用基本不等式求最值,法二,利用导数求最值,无论用哪种方法都应注意函数的定义域;第二问,令
的最值是本问的关键,法一,利用基本不等式求最值,法二,利用导数求最值,无论用哪种方法都应注意函数的定义域;第二问,令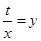 ,将
,将 进行转化,化简成
进行转化,化简成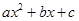 的形式,利用二次函数的单调性求
的形式,利用二次函数的单调性求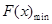 .
.
试题解析:(1)(解法一)
设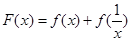
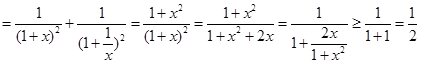 ,
,
∴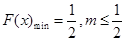 ,∴
,∴ 的最大值为
的最大值为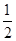 .
.
(解法二)设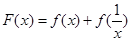
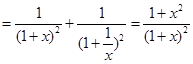 ,
,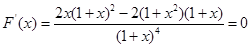 ,
,
∴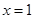 ,当
,当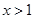 时,
时,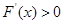 ,当
,当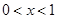 时,
时,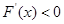 ,∴
,∴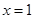 为极小值点,
为极小值点,
∴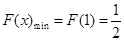 ,∴
,∴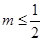 ,∴
,∴ 的最大值为
的最大值为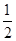 .
.
(2)设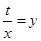 ,则
,则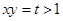 ,则
,则
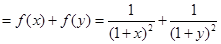
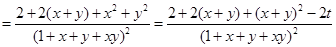
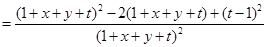
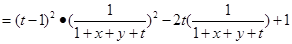
令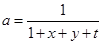 ,则
,则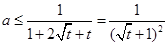
即 ,
,
设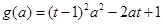 ,∵
,∵ 其对称轴
其对称轴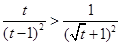 ,
, 在
在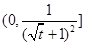 上单调递减,∴
上单调递减,∴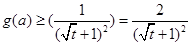 ,
,
∴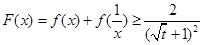 ,
,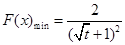 .
.
考点:1.恒成立问题;2.基本不等式;3.利用导数求函数的单调区间和最值;4.二次函数的单调性和最值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
某地开发了一个旅游景点,第1年的游客约为100万人,第2年的游客约为120万人.某数学兴趣小组综合各种因素预测:①该景点每年的游客人数会逐年增加;②该景点每年的游客都达不到130万人.该兴趣小组想找一个函数 来拟合该景点对外开放的第
来拟合该景点对外开放的第
 年与当年的游客人数
年与当年的游客人数 (单位:万人)之间的关系.
(单位:万人)之间的关系.
(1)根据上述两点预测,请用数学语言描述函数 所具有的性质;
所具有的性质;
(2)若 =
= ,试确定
,试确定 的值,并考察该函数是否符合上述两点预测;
的值,并考察该函数是否符合上述两点预测;
(3)若 =
= ,欲使得该函数符合上述两点预测,试确定
,欲使得该函数符合上述两点预测,试确定 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com