
【题目】函数f(x)=5 ![]() +
+ ![]() 的定义域为( )
的定义域为( )
A.{x|1<x≤2}
B.{x|1≤x≤2}
C.{x|x≤2且x≠1}
D.{x|x≥0且x≠1}
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}满足a3=2,前3项和为S3=![]() .
.
(1)求{an}的通项公式;
(2)设等比数列{bn}满足b1=a1,b4=a15,求{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示),规定80分及以上者晋级成功,否则晋级失败(满分为100分).
晋级成功 | 晋级失败 | 合计 | |
男 | 16 | ||
女 | 50 | ||
合计 |
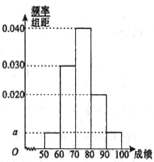
(Ⅰ)求图中![]() 的值;
的值;
(Ⅱ)根据已知条件完成下面![]() 列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
(Ⅲ)将频率视为概率,从本次考试的所有人员中,随机抽取4人进行约谈,记这4人中晋级失败的人数为![]() ,求
,求![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
(参考公式:![]() ,其中
,其中![]() )
)
| 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2015高考湖北(理)20】某厂用鲜牛奶在某台设备上生产![]() 两种奶制品.生产1吨
两种奶制品.生产1吨![]() 产品需鲜牛奶2吨,使用设备1小时,获利1000元;生产1吨
产品需鲜牛奶2吨,使用设备1小时,获利1000元;生产1吨![]() 产品需鲜牛奶1.5吨,使用设备1.5小时,获利1200元.要求每天
产品需鲜牛奶1.5吨,使用设备1.5小时,获利1200元.要求每天![]() 产品的产量不超过
产品的产量不超过![]() 产品产量的2倍,设备每天生产
产品产量的2倍,设备每天生产![]() 两种产品时间之和不超过12小时. 假定每天可获取的鲜牛奶数量W(单位:吨)是一个随机变量,其分布列为
两种产品时间之和不超过12小时. 假定每天可获取的鲜牛奶数量W(单位:吨)是一个随机变量,其分布列为
W | 12 | 15 | 18 |
P | 0.3 | 0.5 | 0.2 |
该厂每天根据获取的鲜牛奶数量安排生产,使其获利最大,因此每天的最大获利![]() (单位:元)是一个随机变量.
(单位:元)是一个随机变量.
(Ⅰ)求![]() 的分布列和均值;
的分布列和均值;
(Ⅱ) 若每天可获取的鲜牛奶数量相互独立,求3天中至少有1天的最大获利超过10000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,有下列说法:
①若f(a)f(b)>0,则函数y=f(x)在区间(a,b)上没有零点;
②若f(a)f(b)>0,则函数y=f(x)在区间(a,b)上可能有零点;
③若f(a)f(b)<0,则函数y=f(x)在区间(a,b)上没有零点;
④若f(a)f(b)<0,则函数y=f(x)在区间(a,b)上至少有一个零点;
其中正确说法的序号是(把所有正确说法的序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点![]() 到点
到点![]() 和直线l:
和直线l: ![]() 的距离相等.
的距离相等.
(Ⅰ)求动点![]() 的轨迹E的方程;
的轨迹E的方程;
(Ⅱ)已知不与![]() 垂直的直线
垂直的直线![]() 与曲线E有唯一公共点A,且与直线
与曲线E有唯一公共点A,且与直线![]() 的交点为
的交点为![]() ,以AP为直径作圆
,以AP为直径作圆![]() .判断点
.判断点![]() 和圆
和圆![]() 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国Ⅳ标准规定:轻型汽车的屡氧化物排放量不得超过80mg/km.根据这个标准,检测单位从某出租车公司运营的A、B两种型号的出租车中分别抽取5辆,对其氮氧化物的排放量进行检测,检测结果记录如表(单位:mg/km)
A | 85 | 80 | 85 | 60 | 90 |
B | 70 | x | 95 | y | 75 |
由于表格被污损,数据x,y看不清,统计员只记得A、B两种出租车的氮氧化物排放量的平均值相等,方差也相等.
(1)求表格中x与y的值;
(2)从被检测的5辆B种型号的出租车中任取2辆,记“氮氧化物排放量超过80mg/km”的车辆数为X,求X=1时的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com