
椭圆![]() 过点P
过点P![]() ,且离心率为
,且离心率为![]() ,F为椭圆的右焦点,
,F为椭圆的右焦点,![]() 、
、![]() 两点在椭圆
两点在椭圆![]() 上,且
上,且 ![]() ,定点
,定点![]() (-4,0).
(-4,0).
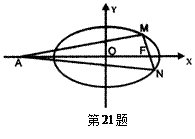 (Ⅰ)求椭圆C的方程;
(Ⅰ)求椭圆C的方程;
(Ⅱ)求证:当![]() 时 ,
时 ,![]() ;
;
(Ⅲ)当![]() 、
、![]() 两点在
两点在![]() 上运动,且
上运动,且![]() =6
=6![]() 时, 求直线MN的方程
时, 求直线MN的方程
(Ⅰ)![]() (Ⅲ)
(Ⅲ)![]() 或
或![]()
(Ⅰ)![]() 椭圆的离心率为
椭圆的离心率为![]()
即![]() 可得
可得![]() --2分
--2分
又椭圆![]() 过点P
过点P![]()
![]()
解得![]() ,
,![]() ,椭圆C的方程为
,椭圆C的方程为![]() -----
-----![]() -----------4分
-----------4分
(Ⅱ)设![]() ,
,
则![]() ,
,
当![]() 时,
时,![]() , -----------5分
, -----------5分
由M,N两点在椭圆上,
![]() ---------6分
---------6分
若![]() ,则
,则![]() (舍去),
(舍去),![]() ------------7分
------------7分
![]() . ------------8分
. ------------8分
(Ⅲ)因为![]() =6
=6![]() .--9分
.--9分
由已知点F(2,0), 所以|AF|=6, 即得|yM-yN|=![]() ------------10分
------------10分
当MN![]() 轴时,
轴时,![]() 故直线的斜率存在. ------------11分
故直线的斜率存在. ------------11分
不妨设直线MN的方程为:![]() -----
-----![]()
联立![]() 、
、![]() 得
得![]() ------------12分
------------12分
![]() |
|![]() |=
|=![]() 解得
解得![]() ------------13分
------------13分
此时,直线MN的方程为![]() 或
或![]() ------------14分
------------14分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
 (2013•丽水一模)已知中心在坐标原点,焦点在x轴上的椭圆过点P(2,3),且它的离心率e=
(2013•丽水一模)已知中心在坐标原点,焦点在x轴上的椭圆过点P(2,3),且它的离心率e=| 1 |
| 2 |
| OM |
| ON |
| OC |
查看答案和解析>>
科目:高中数学 来源:浙江省台州市四校2012届高三第一次联考数学理科试题 题型:044
椭圆![]() 过点P
过点P![]() ,且离心率为
,且离心率为![]() ,F为椭圆的右焦点,M、N两点在椭圆C上,且
,F为椭圆的右焦点,M、N两点在椭圆C上,且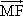 =λ
=λ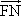 (λ>0),定点A(-4,0).
(λ>0),定点A(-4,0).
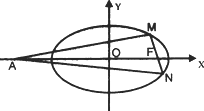
(Ⅰ)求椭圆C的方程;
(Ⅱ)当λ=1时,问:MN与AF是否垂直;并证明你的结论.
(Ⅲ)当M、M两点在C上运动,且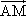 ·
·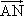 tan∠MAN=6
tan∠MAN=6![]() 时,求直线MN的方程.
时,求直线MN的方程.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省台州市四校高三第一次联考理科数学试卷 题型:解答题
(本小题满分14分)
椭圆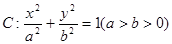 过点P
过点P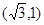 ,且离心率为
,且离心率为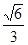 ,F为椭圆的右焦点,
,F为椭圆的右焦点,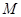 、
、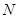 两点在椭圆
两点在椭圆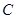 上,且
上,且
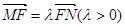 ,定点
,定点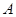 (-4,0).
(-4,0).
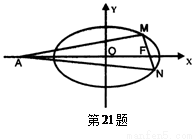
(Ⅰ)求椭圆C的方程;
(Ⅱ)当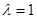 时
,问:MN与AF是否垂直;并证明你的结论.
时
,问:MN与AF是否垂直;并证明你的结论.
(Ⅲ)当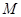 、
、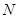 两点在
两点在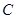 上运动,且
上运动,且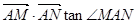 =6
=6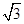 时, 求直线MN的方程.
时, 求直线MN的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
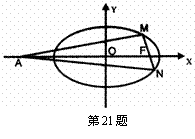
椭圆![]() 过点P
过点P![]() ,且离心率为
,且离心率为![]() ,F为椭圆的右焦点,
,F为椭圆的右焦点,![]() 、
、![]() 两点在椭圆
两点在椭圆![]() 上,且
上,且 ![]() ,定点
,定点![]() (-4,0).
(-4,0).
(Ⅰ)求椭圆C的方程;
(Ⅱ)当![]() 时 ,问:MN与AF是否垂直;并证明你的结论.
时 ,问:MN与AF是否垂直;并证明你的结论.
(Ⅲ)当![]() 、
、![]() 两点在
两点在![]() 上运动,且
上运动,且![]() =6
=6![]() 时,求直线MN的方程.
时,求直线MN的方程.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com