已知指数函数y=f(x)的图象经过点(2,4),且g(x)=|f(x)-1|.
(Ⅰ)作出函数g(x)的图象,并指出它的单调区间及单调性;
(Ⅱ)已知方程g(x-1)=k+2有且仅有一个不同的实数解,求实数k的取值范围.
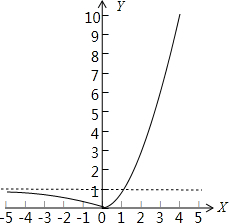
解:(I)设y=f(x)=a
x,代入点(2,4)
得4=a
2,
∴α=2,
∴f(x)=2
x∵函数g(x)=|f(x)-1|,
故将函数f(x)的图象向下平移一个单位,再做纵向的对折变换可得函数g(x)的图象,
由图可得,函数g(x)的有两个单调区间(-∞,0],[0,+∞)
在区间(-∞,0]上函数为减函数,
在区间[0,+∞)上函数为增函数;
(II)函数y=g(x-1)的图象由函数g(x)的图象向右平移两个单位得到
若方程g(x-1)=k+2有且仅有一个不同的实数解,
则函数y=g(x-1)与y=k+2有且仅有一个交点,
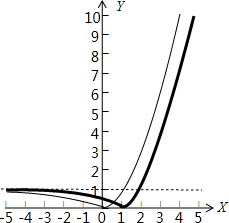
由图可得k+2=0或k+2>1,
故实数k的取值范围为k=-2或k>-1,
分析:(I)利用待定系数法,设f(x)=x
α,代入点(2,4),解指数方程即可得α值,进而求出函数f(x)的解析式,进而利用平移变换法则及对折变换法则,画出函数g(x)的图象,根据图象可分析出函数的单调区间及单调性;
(II)若方程g(x-1)=k+2有且仅有一个不同的实数解,则函数y=g(x-1)与y=k+2有且仅有一个交点,数形结合可得答案.
点评:本题以函数的单调性及单调区间的求法及方程根的个数为载体考查了指数函数解析式的求法,指数函数的图象,函数图象平移变换及对折变换,是函数图象和性质是综合应用.

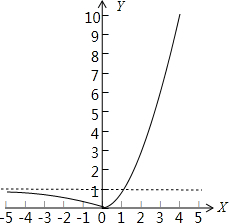 解:(I)设y=f(x)=ax,代入点(2,4)
解:(I)设y=f(x)=ax,代入点(2,4)

