
已知函数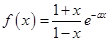 ,若对任意
,若对任意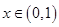 恒有
恒有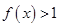 ,求
,求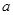 的取值范围。
的取值范围。
解:f(x)的定义域为(-∞,1)∪(1,+∞),对f(x)求导数得 f '(x)= e-ax.
当0<a 2时, f '(x)>0, f(x)在(-∞,1)和(1,+∞)为增函数.,对任意x∈(0,1)恒有f(x)>f(0)=1;
2时, f '(x)>0, f(x)在(-∞,1)和(1,+∞)为增函数.,对任意x∈(0,1)恒有f(x)>f(0)=1;
当a>2时, 利用导数易得:f(x)在(-∞, -), (,1), (1,+∞)为增函数, f(x)在(-,)为减函数,取x0= ∈(0,1),则由(Ⅰ)知 f(x0)<f(0)=1;
当a≤0时, 对任意x∈(0,1),恒有 >1且e-ax≥1,得 f(x)= e-ax≥ >1.;
综上当且仅当a∈(-∞,2)时,对任意x∈(0,1)恒有f(x)>1。
【解析】略


 能力评价系列答案
能力评价系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com