Question

已知圆(x＋4)²＋y²＝25的圆心为M₁，圆(x－4)²＋y²＝1的圆心为M₂，一动圆与这两个圆都外切．w.w.w.k.s.5.u.c.o.m        

⑴求动圆圆心P的轨迹方程；

⑵若过点M₂的直线与⑴中所求轨迹有两个交点A、B，求|AM₁|?|BM₁|的取值范围．

Answer 1

解析：（1）∵|PM₁|－5＝|PM₂|－1，∴|PM₁| － |PM₂|＝4

∴动圆圆心P的轨迹是以M₁、M₂为焦点的双曲线的右支。

c＝4，a＝2，b²＝12，

故所求轨迹方程为－＝1（x≥2）。

（2）当过M₂的直线倾斜角不等于时，设其斜率为k，

直线方程为   y＝k(x－4)

与双曲线  3x²－y²－12＝0联立，消去y化简得(3－k²)x²＋8k²x－16k²－12＝0

又设A(x₁，y₁)，B(x₂，y₂)，x₁>0，x₂>0

由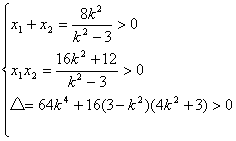解得  k²>3。

由双曲线左准线方程  x＝－1且e＝2，有|AM₁|?|BM₁|＝e|x₁＋1|?e|x₂＋1|＝4[x₁x₂＋(x₁＋x₂)＋1]

＝4(＋＋1)＝100＋ 

w.w.w.k.s.5.u.c.o.m        

∵k²－3>0，∴|AM₁|×|BM₁|>100

又当直线倾斜角等于时，A(4，y₁)，B(4，y₂)，|AM₁|＝|BM₁|＝e(4＋1)＝10

|AM₁|?|BM₁|＝100         故  |AM₁|?|BM₁|≥100。