
【题目】 如图所示的几何体中, ![]() ,
,![]() 平面
平面![]() ,且
,且![]() 平面
平面![]() ,正方形
,正方形![]() 的边长为2,
的边长为2,![]() 为棱
为棱![]() 中点,平面
中点,平面![]() 分别与棱
分别与棱![]() 交于点
交于点![]() .
.

(Ⅰ)求证:![]() ;
;
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)求![]() 的长.
的长.
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中常数
,其中常数![]()
(1)当![]() 时,讨论
时,讨论![]() 的单调性
的单调性
(2)当![]() 时,是否存在整数
时,是否存在整数![]() 使得关于
使得关于![]() 的不等式
的不等式![]() 在区间
在区间![]() 内有解?若存在,求出整数
内有解?若存在,求出整数![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:①对于独立性检验,![]() 的值越大,说明两事件相关程度越大,②以模型
的值越大,说明两事件相关程度越大,②以模型![]() 去拟合一组数据时,为了求出回归方程,设
去拟合一组数据时,为了求出回归方程,设![]() ,将其变换后得到线性方程
,将其变换后得到线性方程![]() ,则
,则![]() 的值分别是
的值分别是![]() 和
和![]() ,③某中学有高一学生400人,高二学生300人,高三学生200人,学校团委欲用分层抽样的方法抽取18名学生进行问卷调查,则高一学生被抽到的概率最大,④通过回归直线
,③某中学有高一学生400人,高二学生300人,高三学生200人,学校团委欲用分层抽样的方法抽取18名学生进行问卷调查,则高一学生被抽到的概率最大,④通过回归直线![]() =
=![]()
![]() +
+![]() 及回归系数
及回归系数![]() ,可以精确反映变量的取值和变化趋势,其中正确的个数是
,可以精确反映变量的取值和变化趋势,其中正确的个数是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象中相邻两条对称轴之间的距离为
的图象中相邻两条对称轴之间的距离为![]() ,且直线
,且直线![]() 是其图象的一条对称轴.
是其图象的一条对称轴.

(1)求![]() ,
,![]() 的值;
的值;
(2)在图中画出函数![]() 在区间
在区间![]() 上的图象;
上的图象;
(3)将函数![]() 的图象上各点的横坐标缩短为原来的
的图象上各点的横坐标缩短为原来的![]() (纵坐标不变),再把得到的图象向左平移
(纵坐标不变),再把得到的图象向左平移![]() 个单位,得到
个单位,得到![]() 的图象,求
的图象,求![]() 单调减区间.
单调减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
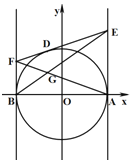
【题目】如图所示,圆O:![]() ,
,![]() ,
,![]() ,D为圆O上任意一点,过D作圆O的切线分别交直线
,D为圆O上任意一点,过D作圆O的切线分别交直线![]() 和
和![]() 于E,F两点,连AF,BE交于点G,若点G形成的轨迹为曲线C.
于E,F两点,连AF,BE交于点G,若点G形成的轨迹为曲线C.
![]() 记AF,BE斜率分别为
记AF,BE斜率分别为![]() ,
,![]() ,求
,求![]() 的值并求曲线C的方程;
的值并求曲线C的方程;
![]() 设直线l:
设直线l:![]() 与曲线C有两个不同的交点P,Q,与直线
与曲线C有两个不同的交点P,Q,与直线![]() 交于点S,与直线
交于点S,与直线![]() 交于点T,求
交于点T,求![]() 的面积与
的面积与![]() 面积的比值
面积的比值![]() 的最大值及取得最大值时m的值.
的最大值及取得最大值时m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以
为参数),在以![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 是圆心在极轴上,且经过极点的圆.已知曲线
是圆心在极轴上,且经过极点的圆.已知曲线![]() 上的点
上的点![]() 对应的参数
对应的参数![]() ,射线
,射线![]() 与曲线
与曲线![]() 交于点
交于点![]()
(1)求曲线![]() 、
、![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 在曲线
在曲线![]() 上的两个点且
上的两个点且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】打赢扶贫攻坚战,到2020年全面建成小康社会,是中国共产党向全世界和全国人民的承诺.一贫困户在政府扶持下结合地方特色联合当地几户贫困户创办一家农产品公司.为了振兴乡村,打好扶贫攻坚战,某市党政府开展了地标特产展销会.该公司拟定在2020年元旦展销期间举行产品促销活动,经测算该产品的年销量t万件(生产量与销量相等)与促销费用x万元满足![]() 已知2020年生产该产品还需投入成本4+t万元(不含促销费),促销费x满足当
已知2020年生产该产品还需投入成本4+t万元(不含促销费),促销费x满足当![]() 产品销量价格定为5元/件,当
产品销量价格定为5元/件,当![]() 产品销量价格定为
产品销量价格定为![]() 元/件(其中a为正常数).
元/件(其中a为正常数).
(1)试将2020年该产品的利润y万元表示为促销费费x万元的函数;
(2)2020年该公司促销费投入多少万元时,公司利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,点E,F,G分别为线段BC,PB,AD的中点.

(1)证明:EF∥平面PAC;
(2)证明:平面PCG∥平面AEF;
(3)在线段BD上找一点H,使得FH∥平面PCG,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com