
【题目】如图(示意),公路AM、AN围成的是一块顶角为钝角α的角形耕地,其中![]() .在该块土地中
.在该块土地中![]() 处有一小型建筑,经测量,它到公路
处有一小型建筑,经测量,它到公路![]() 、
、![]() 的距离
的距离![]() 、
、![]() 分别为
分别为![]() ,
,![]() .现要过点
.现要过点![]() 修建一条直线公路
修建一条直线公路![]() ,将三条公路围成的区域
,将三条公路围成的区域![]() 建成一个工业园.设
建成一个工业园.设![]() ,
,![]()
![]() ,其中
,其中![]() .
.

(1)试建立![]() 间的等量关系;
间的等量关系;
(2)为尽量减少耕地占用,问如何确定B点的位置,使得该工业园区的面积最小?并求最小面积.
【答案】(1)3x+2y=![]() xy;(2)当AB=10km时,最小面积为30km2
xy;(2)当AB=10km时,最小面积为30km2
【解析】
(1)过点P作PE⊥AM,PF⊥AN,垂足为E、F,连接PA.设AB=x,AC=y.由S△ABC=S△ABP+S△APC,求得面积的表达式,从而求得x,y的关系.
(2)运用基本不等式可得最小值.
(1)过点P作PE⊥AM,PF⊥AN,垂足为E、F.因为P到AM,AN的距离分别为3,2,
即PE=3,PF=2.由S△ABC=S△ABP+S△APC=![]() x3
x3![]() y2=
y2=![]() (3x+2y)①
(3x+2y)①
所以S△ABC=![]() xy② ,即3x+2y=
xy② ,即3x+2y=![]() xy.
xy.
(2)因为3x+2y≥2![]() ,所以
,所以![]() xy≥2
xy≥2![]() .解得xy≥150.
.解得xy≥150.
当且仅当3x=2y取“=”,即x=10,y=15.
所以S△ABC=![]() xy有最小值30.
xy有最小值30.
所以:当AB=10km时,该工业园区的面积最小,最小面积为30km2


科目:高中数学 来源: 题型:
【题目】某中学共有1000名学生参加了该地区高三第一次质量检测的数学考试,数学成绩如下表所示:
数学成绩分组 | [0,30) | [30,60) | [60,90) | [90,120) | [120,150] |
人数 | 60 | 90 | 300 | x | 160 |
(Ⅰ)为了了解同学们前段复习的得失,以便制定下阶段的复习计划,学校将采用分层抽样的方法抽取100名同学进行问卷调查,甲同学在本次测试中数学成绩为95分,求他被抽中的概率;
(Ⅱ)作出频率分布直方图,并估计该学校本次考试的数学平均分.(同一组中的数据用该组区间的中点值作代表)
查看答案和解析>>
科目:高中数学 来源: 题型:
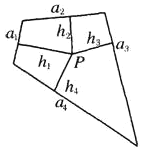
【题目】如图所示,面积为![]() 的平面凸四边形的第
的平面凸四边形的第![]() 条边的边长记为
条边的边长记为![]() ,此四边形内任一点
,此四边形内任一点![]() 到第
到第![]() 条边的距离记为
条边的距离记为![]() ,若
,若![]() ,则
,则![]() .类比以上性质,体积为
.类比以上性质,体积为![]() 的三棱锥的第
的三棱锥的第![]() 个面的面积记为
个面的面积记为![]() ,此三棱锥内任一点
,此三棱锥内任一点![]() 到第
到第![]() 个面的距离记为
个面的距离记为![]() ,若
,若![]() ,则
,则![]() 等于( )
等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,且过点(1,
,且过点(1,![]() ).
).
(1)求椭圆C的方程;
(2)设与圆O:x2+y2=![]() 相切的直线l交椭圆C于A,B两点,求△OAB面积的最大值,及取得最大值时直线l的方程.
相切的直线l交椭圆C于A,B两点,求△OAB面积的最大值,及取得最大值时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知不等式ax2-5x+b>0的解是-3<x<2,设A={x|bx2-5x+a>0},B={x|![]() }.
}.
(1)求a,b的值;
(2)求A∩B和A∪(UB).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家射击队的某队员射击一次,命中7~10环的概率如表所示:
命中环数 | 10环 | 9环 | 8环 | 7环 |
概率 | 0.32 | 0.28 | 0.18 | 0.12 |
求该射击队员射击一次 求:
(1)射中9环或10环的概率;
(2)至少命中8环的概率;(3)命中不足8环的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,多面体ABCDEF中,四边形ABCD为矩形,二面角A-CD-F为60°,DE∥CF,CD⊥DE,AD=2,DE=DC=3,CF=6.

(1)求证:BF∥平面ADE;
(2)在线段CF上求一点G,使锐二面角B-EG-D的余弦值为![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com