
已知向量![]() =(x2-3,1),
=(x2-3,1),![]() =(x,-y),(其中实数x和y不同时为零),当|x|<2时,有
=(x,-y),(其中实数x和y不同时为零),当|x|<2时,有![]() ⊥
⊥![]() ,当|x|≥2时,
,当|x|≥2时,![]() ∥
∥![]() .
.
(1)求函数式y=f(x);
(2)求函数f(x)的单调递减区间;
(3)若对![]() x∈(-∞,-2]∪[2,+∞),都有mx2+x-3m≥0,求实数m的取值范围.
x∈(-∞,-2]∪[2,+∞),都有mx2+x-3m≥0,求实数m的取值范围.
科目:高中数学 来源:山东省聊城市水城中学2011-2012学年高二下学期阶段测试(二)数学理科试题 题型:013
已知向量 =(3,-2),
=(3,-2),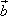 =(x+1,2-x2),则条件“x=2”是条件“a∥b”成立的
=(x+1,2-x2),则条件“x=2”是条件“a∥b”成立的
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件.
查看答案和解析>>
科目:高中数学 来源:浙江省杭州学军中学2012届高三第二次月考数学文科试题 题型:022
已知向量![]() =(x1,y1),
=(x1,y1),![]() =(x2,y2),
=(x2,y2),![]() =(x3,y3),定义运算“*”的意义为
=(x3,y3),定义运算“*”的意义为![]() *
*![]() =(x1y2,x2y1).则下列命题①若
=(x1y2,x2y1).则下列命题①若![]() =(1,2),
=(1,2),![]() =(3,4),则
=(3,4),则![]() *
*![]() =(6,4)
=(6,4)
②![]() *
*![]() =
=![]() *
*![]()
③(![]() *
*![]() )*
)*![]() =
=![]() *(
*(![]() *
*![]() )
)
④(![]() +
+![]() )*
)*![]() =(
=(![]() *
*![]() )+(
)+(![]() *
*![]() )中,正确的是________.
)中,正确的是________.
查看答案和解析>>
科目:高中数学 来源:江西省南昌二中2012届高三第四次月考数学理科试题 题型:044
已知向量![]() =(x2-3,1),
=(x2-3,1),![]() =(x,-y),(其中实数x和y不同时为零),当|x|<2时,有
=(x,-y),(其中实数x和y不同时为零),当|x|<2时,有![]() ⊥
⊥![]() ,当|x|≥2时,
,当|x|≥2时,![]() ∥
∥![]() .
.
(1)求函数式y=f(x);
(2)若对![]() x∈(-∞,-2)∪[2,+∞),都有mx2+x-3m≥0,求实数m的取值范围.
x∈(-∞,-2)∪[2,+∞),都有mx2+x-3m≥0,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014届四川绵阳南山中学高一5月月考数学试卷(解析版) 题型:选择题
已知向量 =(x1,y1),
=(x1,y1), =(x2,y2),若|
=(x2,y2),若| |=2,|
|=2,| |=3,
|=3, ·
· =-6,则
=-6,则  的值为
( )
的值为
( )
A.  B.
B. C.
C.  D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com