
在△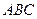 中,内角
中,内角 ,
,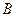 ,
, 对边的边长分别是
对边的边长分别是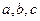 ,已知
,已知 .
.
(1)若△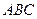 的面积等于
的面积等于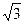 ,求
,求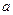 ,
,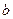 ;
;
(2)若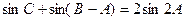 ,求△
,求△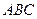 的面积.
的面积.
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:解答题
(本小题满分13分)
设 的BC边上的高AD=BC,a,b,c分别是内角A,B,C的对边。
的BC边上的高AD=BC,a,b,c分别是内角A,B,C的对边。
(1)求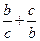 的最小值及取得最小值时
的最小值及取得最小值时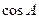 的值;
的值;
(2)把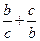 表示为
表示为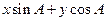 的形式,判断
的形式,判断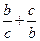 能否等于
能否等于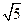 ?并说明理由。
?并说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)在△ABC中,已知内角A、B、C所对的边分别为a、b、c,
且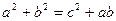
(1) 若 ,且
,且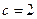 ,求
,求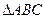 的面积;
的面积;
(2)已知向量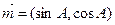 ,
,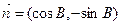 ,求|
,求|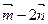 |的取值范围.
|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
((本小题满分12分)
炮兵阵地位于地面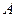 处,两观察所分别位于地面点
处,两观察所分别位于地面点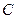 和
和 处,已知
处,已知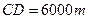 ,
, 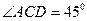 ,
,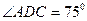 , 目标出现于地面点
, 目标出现于地面点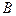 处时,测得
处时,测得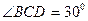 ,
,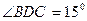 (如答题卷图所示).求:炮兵阵地到目标的距离.
(如答题卷图所示).求:炮兵阵地到目标的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题12分)一缉私艇发现在方位角45°方向,距离12海里的海面上有一走私船正以10海里/小时的速度沿方位角为105°方向逃窜,若缉私艇的速度为14海里/小时,缉私艇沿方位角45°+α的方向追去,若要在最短的时间内追上该走私船,求追击所需时间和α角的正弦.(注:方位角是指正北方向按顺时针方向旋转形成的角,设缉私艇与走私船原来的位置分别为A、C,在B处两船相遇). 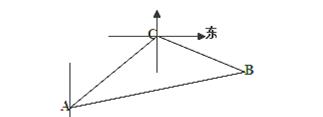
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com