
【题目】已知函数f(x)= ![]() .
.
(1)用定义证明函数f(x)在(﹣∞,+∞)上为减函数;
(2)若x∈[1,2],求函数f(x)的值域;
(3)若g(x)= ![]() ,且当x∈[1,2]时g(x)≥0恒成立,求实数a的取值范围.
,且当x∈[1,2]时g(x)≥0恒成立,求实数a的取值范围.
【答案】
(1)证明:设x1<x2,
则f(x1)﹣f(x2)= ![]() ﹣
﹣ 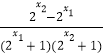
∵x1<x2,∴2x2﹣2x1>0
又2x1+1>0,2x2+1>0,
f(x1)﹣f(x2)>0即f(x1)>f(x2)
∴f(x)在(﹣∞,+∞)上为减函数
(2)解:∵f(x)在(﹣∞,+∞)上为减函数,
∴f(x)值域为 ![]()
(3)解:当x∈[{1,2}]时,g(x)∈ ![]()
∵g(x)≥0在x∈[1,2]上恒成立,
∴ ![]() ,∴
,∴ ![]()
【解析】(1)根据函数单调性的定义,先在所给区间上任设两个数并确定好大小,然后通过作差法即可获得自变量对应函数值的大小关系,由定义即可获得问题的解答;(2)结合(1)所证明的结论即可获得函数在[1,2]上的单调性,从而可以求的函数在[1,2]上的最值,进而问题即可获得解答;(3)充分利用前两问答结论,即可获得g(x)= ![]() 在[1,2]上的最值,结合恒成立的条件即可将问题转化为实数a的不等关系,求解即可获得问题的解答.
在[1,2]上的最值,结合恒成立的条件即可将问题转化为实数a的不等关系,求解即可获得问题的解答.
【考点精析】认真审题,首先需要了解函数的值域(求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的),还要掌握函数单调性的判断方法(单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较)的相关知识才是答题的关键.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x+ ![]() (x≠0).
(x≠0).
(1)判断并证明函数在其定义域上的奇偶性;
(2)判断并证明函数在(2,+∞)上的单调性;
(3)解不等式f(2x2+5x+8)+f(x﹣3﹣x2)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的圆心在直线
的圆心在直线![]() :
: ![]() 上,与直线
上,与直线![]() :
: ![]() 相切,且截直线
相切,且截直线![]() :
: ![]() 所得弦长为6
所得弦长为6
(Ⅰ)求圆![]() 的方程
的方程
(Ⅱ)过点![]() 是否存在直线
是否存在直线![]() ,使以
,使以![]() 被圆
被圆![]() 截得弦
截得弦![]() 为直径的圆经过原点?若存在,写出直线的方程;若不存在,说明理由.
为直径的圆经过原点?若存在,写出直线的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图![]() 是直三棱柱,底面
是直三棱柱,底面![]() 是等腰直角三角形,且
是等腰直角三角形,且![]() ,直三棱柱的高等于4,线段
,直三棱柱的高等于4,线段![]() 的中点为
的中点为![]() ,线段
,线段![]() 的中点为
的中点为![]() ,线段
,线段![]() 的中点为
的中点为![]() .
.
(1)求异面直线![]() 、
、![]() 所成角的大小;
所成角的大小;
(2)求三棱锥![]() 的体积.
的体积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(I)求函数![]() 的对称轴方程;
的对称轴方程;
(II)将函数![]() 的图象上各点的纵坐标保持不变,横坐标伸长为原来的2倍,然后再向左平移
的图象上各点的纵坐标保持不变,横坐标伸长为原来的2倍,然后再向左平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象.若
的图象.若![]() 分别是△ABC三个内角A,B,C的对边,a=2,c=4,且
分别是△ABC三个内角A,B,C的对边,a=2,c=4,且![]() ,求b的值.
,求b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(I)求函数![]() 的对称轴方程;
的对称轴方程;
(II)将函数![]() 的图象上各点的纵坐标保持不变,横坐标伸长为原来的2倍,然后再向左平移
的图象上各点的纵坐标保持不变,横坐标伸长为原来的2倍,然后再向左平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象.若
的图象.若![]() 分别是△ABC三个内角A,B,C的对边,a=2,c=4,且
分别是△ABC三个内角A,B,C的对边,a=2,c=4,且![]() ,求b的值.
,求b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】分层抽样是将总体分成互不交叉的层,然后按照一定的比例,从各层独立地抽取一定数量的个体,组成一个样本的抽样方法;在《九章算术》第三章“衰分”中有如下问题:“今有甲持钱五百六十,乙持钱三百五十,丙持钱一百八十,凡三人俱出关,关税百钱.欲以钱多少衰出之,问各几何?”其译文为:今有甲持560钱,乙持350钱,丙持180钱,甲、乙、丙三人一起出关,关税共100钱,要按照各人带钱多少的比例进行交税,问三人各应付多少税?则下列说法错误的是( )
A. 甲应付![]() 钱 B. 乙应付
钱 B. 乙应付![]() 钱
钱
C. 丙应付![]() 钱 D. 三者中甲付的钱最多,丙付的钱最少
钱 D. 三者中甲付的钱最多,丙付的钱最少
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农科所发现,一种作物的年收获量 ![]() (单位:
(单位: ![]() )与它“相近”作物的株数
)与它“相近”作物的株数 ![]() 具有线性相关关系(所谓两株作物“相近”是指它们的直线距离不超过
具有线性相关关系(所谓两株作物“相近”是指它们的直线距离不超过 ![]() ),并分别记录了相近作物的株数为
),并分别记录了相近作物的株数为 ![]() 时,该作物的年收获量的相关数据如下:
时,该作物的年收获量的相关数据如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|

(1)求该作物的年收获量 ![]() 关于它“相近”作物的株数
关于它“相近”作物的株数![]() 的线性回归方程;
的线性回归方程;
(2)农科所在如图所示的正方形地块的每个格点(指纵、横直线的交叉点)处都种了一株该作物,其中每
个小正方形的面积为 ![]() ,若在所种作物中随机选取一株,求它的年收获量的分布列与数学期望.(注:年收
,若在所种作物中随机选取一株,求它的年收获量的分布列与数学期望.(注:年收
获量以线性回归方程计算所得数据为依据)
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估
的斜率和截距的最小二乘估
计分别为, 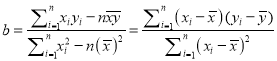 ,
, ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com