Question

【题目】如图，四棱锥P－ABCD中，AD⊥平面PAB，AP⊥AB．

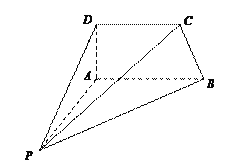
（1）求证：CD⊥AP；

（2）若CD⊥PD，求证：CD∥平面PAB；

Answer 1

【答案】（1）见解析;（2）见解析.

【解析】试题分析：（1）由平面，得到，由，进而证得平面，即可证明；

（2）首先证得平面， 平面，得到，利用直线与平面平行的判定定理，即可证得结论。

试题解析：

（1）因为AD⊥平面PAB，AP平面PAB，

所以AD⊥AP．又因为AP⊥AB ，AB∩AD＝A，AB平面ABCD，AD平面ABCD，

所以AP⊥平面ABCD． 因为CD平面ABCD，

所以CD⊥AP．

（2）因为CD⊥AP，CD⊥PD，且PD∩AP＝P，PD平面PAD，AP平面PAD，

所以CD⊥平面PAD． ①

因为AD⊥平面PAB，AB平面PAB，

所以AB⊥AD．

又因为AP⊥AB，AP∩AD＝A，AP平面PAD，AD平面PAD，

所以AB⊥平面PAD． ②

由①②得CD∥AB，

因为CD平面PAB，AB平面PAB，

所以CD∥平面PAB．