Question

已知a为常数，求函数f（x）=-x³+3ax（0≤x≤1）的最大值．

Answer 1

分析：求函数f（x）=-x³+3ax的导数，对方程f'（x）=-3（x²-a）=0有无实根，和有根，根是否在区间[0，1]内进行讨论，求得函数的极值，再与f（0）、f（1）比较大小，确定函数的最大值．

解答：解：f'（x）=-3x²+3a=-3（x²-a）
若a≤0，则f'（x）=-3（x²-a）≤0，此时函数f（x）单调递减，
所以当x=0时，f（x）取得最大值，f（x）_max=f（0）=0
若a＞0，令f'（x）=-3（x²-a）=0，解得x=±

a

，
∵x∈[0，1]，则只考虑x=

a

的情况，如表所示：

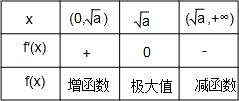
①当0＜a＜1时，根据函数的增减性得，
当x=

a

时，f（x）有最大值，f（x）_max=f（

a

）=2a

a

；
②当

a

≥1，即a≥1时，根据函数的增减性得
当x=1时，f（x）有最大值．f（x）_max=f（1）=3a-1．
综合以上可知：
当a≤0时，x=0，f（x）有最大值0；
当0＜a＜1时，x=

a

，f（x）有最大值2a

a

；
当a≥1时，x=1，f（x）有最大值3a-1．

点评：考查利用导数研究函数在闭区间上的最值问题，对方程f'（x）═0有无实根，和有根，根是否在区间[0，1]内进行讨论，体现了分类讨论的思想方法，增加了题目的难度，属中档题．