
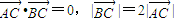 .
.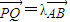 ?请给出证明.
?请给出证明.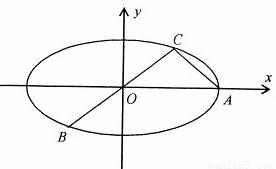
 判断△AOC是等腰直角三角形,进而求得C的坐标代入椭圆的方程求得b,最后可得椭圆的方程.
判断△AOC是等腰直角三角形,进而求得C的坐标代入椭圆的方程求得b,最后可得椭圆的方程. 关系得证.
关系得证. 解:(Ⅰ)设椭圆方程为
解:(Ⅰ)设椭圆方程为 ,
, .
. ,
, .
. 联立得到(3k2+1)x2+6k(1-k)x+3(1-k)2-4=0
联立得到(3k2+1)x2+6k(1-k)x+3(1-k)2-4=0 且k≠0
且k≠0

 且k≠0
且k≠0 ,
,


 ,即总存在实数λ使
,即总存在实数λ使


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
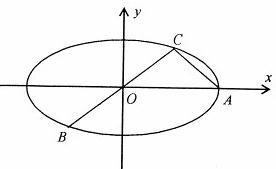 如图:已知椭圆A,B,C是长轴长为4的椭圆上三点,点A是长轴的一个端点,BC过椭圆的中心O,且
如图:已知椭圆A,B,C是长轴长为4的椭圆上三点,点A是长轴的一个端点,BC过椭圆的中心O,且| AC |
| BC |
| BC |
| AC |
| PQ |
| AB |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖北省孝感高中高二(上)期末数学试卷(理科)(解析版) 题型:解答题
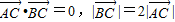 .
.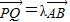 ?请给出证明.
?请给出证明.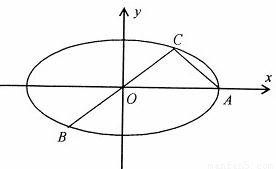
查看答案和解析>>
科目:高中数学 来源:2009-2010学年四川省攀枝花市高三(上)第二次月考数学试卷(理科)(解析版) 题型:解答题
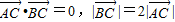 .
.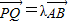 ?请给出证明.
?请给出证明.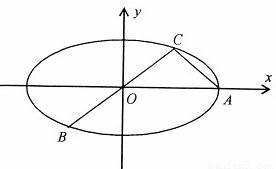
查看答案和解析>>
科目:高中数学 来源:2011年湖北省武汉市武昌区高三五月调考数学试卷(理科)(解析版) 题型:解答题
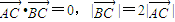 .
.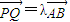 ?请给出证明.
?请给出证明.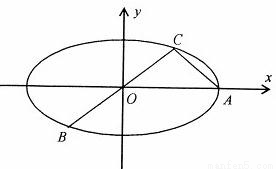
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com