
设函数 的定义域为R,若存在常数M>0,使
的定义域为R,若存在常数M>0,使 对 一切实数x均成 立,则称
对 一切实数x均成 立,则称 为“倍约束函数”,现给出下列函数:①
为“倍约束函数”,现给出下列函数:①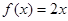 :②
:② :③
:③ ;④
;④ ⑤
⑤ 是定义在实数集R上的奇函数,且
是定义在实数集R上的奇函数,且
对一切 均有
均有 ,其中是“倍约束函数”的有( )
,其中是“倍约束函数”的有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
C
解析试题分析:解:①对于函数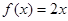 ,存在
,存在 ,使
,使 对 一切实数x均成 立,所以该函数是“倍约束函数”;
对 一切实数x均成 立,所以该函数是“倍约束函数”;
②对于函数 ,当
,当 时,
时, ,故不存在常数M>0,使
,故不存在常数M>0,使 对 一切实数x均成 立,所以该函数不是“倍约束函数”;
对 一切实数x均成 立,所以该函数不是“倍约束函数”;
③对于函数 ,当
,当 时,
时, ,故不存在常数M>0,使
,故不存在常数M>0,使 对 一切实数x均成 立,所以该函数不是“倍约束函数”;
对 一切实数x均成 立,所以该函数不是“倍约束函数”;
④对于函数 ,因为当
,因为当 时,
时, ;
;
当 时,
时, ,所以存在常数
,所以存在常数 ,使
,使 对 一切实数x均成 立, 所以该函数是“倍约束函数”;
对 一切实数x均成 立, 所以该函数是“倍约束函数”;
⑤由题设 是定义在实数集R上的奇函数,
是定义在实数集R上的奇函数, ,所以在
,所以在 中令
中令 ,于是有
,于是有 ,即存在常数
,即存在常数 ,使
,使 对 一切实数x均成 立, 所以该函数是“倍约束函数”;
对 一切实数x均成 立, 所以该函数是“倍约束函数”;
综上可知“倍约束函数”的有①④⑤共三个,所以应选C.
考点:1、新定义;2、赋值法;3、基本初等函数的性质.


科目:高中数学 来源: 题型:单选题
定义方程f(x)=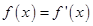 的实数根x0叫做函数f(x)的“新驻点”,若函数g(x)=2x,h(x)=
的实数根x0叫做函数f(x)的“新驻点”,若函数g(x)=2x,h(x)= ,φ(x)=x3(x≠0)的“新驻点”分别为A,b,c,则A,b,c的大小关系为( )
,φ(x)=x3(x≠0)的“新驻点”分别为A,b,c,则A,b,c的大小关系为( )
A. | B. | C. | D. |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
[2014·沈阳模拟]若一根蜡烛长20 cm,点燃后每小时燃烧5 cm,则燃烧剩下的高度h(cm)与燃烧时间t(小时)的函数关系用图象表示为( )
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
某商人如果将进货单价为8元的商品按每件10元出售时,每天可销售100件,现在他采用提高售价,减少进货量的办法增加利润.已知这种商品每件销售价提高1元,销售量就要减少10件,如果使得每天所赚的利润最大,那么他将销售价每件定为( )
| A.11元 | B.12元 | C.13元 | D.14元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com