
【题目】在三棱锥A-BCD中,平面ABC丄平面ADC, AD丄AC,AD=AC, ![]() ,若此三棱锥的外接球表面积为
,若此三棱锥的外接球表面积为![]() ,则三棱锥A-BCD体积的最大值为( )
,则三棱锥A-BCD体积的最大值为( )
A.7B.12C.6D.![]()
【答案】C
【解析】
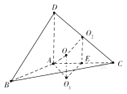
设三棱锥A﹣BCD外接球的半径为R,三棱锥的外接球球心为O,△ABC的外心为O1,△ABC的外接圆半径为r,取DC的中点为O2,过O2作O2E⊥AC,则OO1⊥平面ABC,OO2⊥平面ADC,连结OA,O1A,则O1A=r,设AD=AC=b,则OO1=O2E![]() b,由S=4πR2=28π,解得R
b,由S=4πR2=28π,解得R![]() ,由正弦正理求出b
,由正弦正理求出b![]() ,若三棱锥A﹣BCD的体积最大,则只需△ABC的面积最大,由此能求出三棱锥A﹣BCD的体积的最大值.
,若三棱锥A﹣BCD的体积最大,则只需△ABC的面积最大,由此能求出三棱锥A﹣BCD的体积的最大值.
根据题意,设三棱锥A﹣BCD外接球的半径为R,
三棱锥的外接球球心为O,
△ABC的外心为O1,△ABC的外接圆半径为r,
取DC的中点为O2,过O2作O2E⊥AC,
则OO1⊥平面ABC,OO2⊥平面ADC,
如图,连结OA,O1A,则O1A=r,
设AD=AC=b,则OO1=O2E![]() b,
b,
由S=4πR2=28π,解得R![]() ,
,
在△ABC中,由正弦正理得2r![]() ,
,
∴2r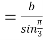 ,解得b
,解得b![]() ,
,
在Rt△OAO1中,7=r2+(![]() )2,解得r=2,b=2
)2,解得r=2,b=2![]() ,∴AC=2
,∴AC=2![]() ,
,
若三棱锥A﹣BCD的体积最大,则只需△ABC的面积最大,
在△ABC中,AC2=AB2+BC2﹣2ABBCcos∠ABC,
∴12=AB2+BC2﹣ABBC≥2ABBC﹣ABBC,
解得ABBC≤12,
∴![]() 3
3![]() ,
,
∴三棱锥A﹣BCD的体积的最大值:
![]() 6.
6.
故选:


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:
【题目】设![]() 、
、![]() 、
、![]() 是集合,称
是集合,称![]() 为有序三元组,如果集合
为有序三元组,如果集合![]() 、
、![]() 、
、![]() 满足
满足![]()
![]() ,且
,且![]() ,则称有序三元组
,则称有序三元组![]() 为最小相交(其中
为最小相交(其中![]() 表示集合
表示集合![]() 中的元素个数),如集合
中的元素个数),如集合![]() ,
,![]() ,
,![]() 就是最小相交有序三元组,则由集合
就是最小相交有序三元组,则由集合![]() 的子集构成的最小相交有序三元组的个数是________
的子集构成的最小相交有序三元组的个数是________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() (
(![]() 为常数).
为常数).
(i)给出下列结论:
①曲线![]() 为中心对称图形;
为中心对称图形;
②曲线![]() 为轴对称图形;
为轴对称图形;
③当![]() 时,若点
时,若点![]() 在曲线
在曲线![]() 上,则
上,则![]() 或
或![]() .
.
其中,所有正确结论的序号是_________.
(ii)当![]() 时,若曲线
时,若曲线![]() 所围成的区域的面积小于
所围成的区域的面积小于![]() ,则
,则![]() 的值可以是_________.(写出一个即可)
的值可以是_________.(写出一个即可)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{2n﹣1}的前n项1,3,7,…,2n﹣1组成集合![]() (n∈N*),从集合An中任取k(k=1,2,3,…,n)个数,其所有可能的k个数的乘积的和为Tk(若只取一个数,规定乘积为此数本身),记Sn=T1+T2+…+Tn,例如当n=1时,A1={1},T1=1,S1=1;当n=2时,A2={1,3},T1=1+3,T2=1×3,S2=1+3+1×3=7,试写出Sn=__.
(n∈N*),从集合An中任取k(k=1,2,3,…,n)个数,其所有可能的k个数的乘积的和为Tk(若只取一个数,规定乘积为此数本身),记Sn=T1+T2+…+Tn,例如当n=1时,A1={1},T1=1,S1=1;当n=2时,A2={1,3},T1=1+3,T2=1×3,S2=1+3+1×3=7,试写出Sn=__.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.

(1) 证明:PB∥平面AEC
(2) 设二面角D-AE-C为60°,AP=1,AD=![]() ,求三棱锥E-ACD的体积
,求三棱锥E-ACD的体积
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某环境保护部门对某处的环境状况用“污染指数”来监测,据测定,该处的“污染指数”与附近污染源的强度和距离之比成正比,比例系数为常数![]()
![]() ,现已知相距
,现已知相距![]() 的
的![]() 两家化工厂(污染源)的污染强度分别为1和
两家化工厂(污染源)的污染强度分别为1和![]()
![]() ,它们连线段上任意一点
,它们连线段上任意一点![]() 处的污染指数
处的污染指数![]() 等于两化工厂对该处的污染指数之和,设
等于两化工厂对该处的污染指数之和,设![]() ;
;
(1)试将![]() 表示为
表示为![]() 的函数,指出其定义域;
的函数,指出其定义域;
(2)当![]() 时,
时,![]() 处的“污染指数”最小,试求
处的“污染指数”最小,试求![]() 化工厂的污染强度
化工厂的污染强度![]() 的值;
的值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() ,
,![]() ,我们知道当a取不同的值时,得到不同的数列.如当
,我们知道当a取不同的值时,得到不同的数列.如当![]() 时,得到无穷数列:0,
时,得到无穷数列:0,![]() ,
,![]() ,
,![]() ,…,当
,…,当![]() 时,得到有穷数列:
时,得到有穷数列:![]() ,
,![]() ,1.
,1.
(1)当a为何值时,![]() ;
;
(2)设数列![]() 满足
满足![]() ,
,![]() ,求证:a取
,求证:a取![]() 中的任一数,都可以得到一个有穷数列
中的任一数,都可以得到一个有穷数列![]() ;
;
(3)是否存在实数a,使得到的![]() 是无穷数列,且对于任意
是无穷数列,且对于任意![]() ,都有
,都有![]() 成立,若存在,求出a的取值范围;若不存在,请说明理由.
成立,若存在,求出a的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由![]() 个不同的数构成的数列
个不同的数构成的数列![]() 中,若
中,若![]() 时,
时,![]() (即后面的项
(即后面的项![]() 小于前面项
小于前面项![]() ),则称
),则称![]() 与
与![]() 构成一个逆序,一个有穷数列的全部逆序的总数称为该数列的逆序数.如对于数列3,2,1,由于在第一项3后面比3小的项有2个,在第二项2后面比2小的项有1个,在第三项1后面比1小的项没有,因此,数列3,2,1的逆序数为
构成一个逆序,一个有穷数列的全部逆序的总数称为该数列的逆序数.如对于数列3,2,1,由于在第一项3后面比3小的项有2个,在第二项2后面比2小的项有1个,在第三项1后面比1小的项没有,因此,数列3,2,1的逆序数为![]() ;同理,等比数列
;同理,等比数列![]() 的逆序数为
的逆序数为![]() .
.
(1)计算数列![]() 的逆序数;
的逆序数;
(2)计算数列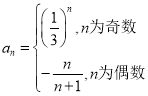 (
(![]() )的逆序数;
)的逆序数;
(3) 已知数列![]() 的逆序数为
的逆序数为![]() ,求
,求![]() 的逆序数.
的逆序数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com