练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知5个乒乓球,其中3个新的,2个旧的,每次取1个,不放回的取两次,  
    求:(1)第一次取到新球的概率．
    (2)第二次取到新球的概率．
    (3)在第一次取到新球的条件下第二次取到新球的概率．

    （1）；（2）；（3）．

    解析试题分析：（1）此问为古典概型的概率，总的基本事件的个数为5个，第一次取到新球的基本事件包含3个，所以;
    (2)第二次取到新球包含两种情况，第一次取到新球，或是第一次没有取到新球；
    （3）此问为条件概率，根据公式
    设第i次取到新球为事件，第j次取到旧球为事件．（i,j=1，2）
    （1）                  4分
    （2） 第二次取到新球为C事件，  
        8分
    （3）                      12分
    考点：1．古典概型的概率问题；2．条件概率．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    （本小题满分14分）
    将连续正整数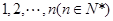从小到大排列构成一个数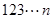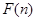，为这个数的位数（如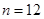时，此数为，共有15个数字，），现从这个数中随机取一个数字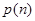，为恰好取到0的概率.
    （1）求；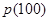
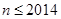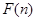    （2）当时，求的表达式；
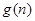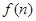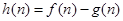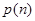    （3）令为这个数中数字0的个数，为这个数中数字9的个数，，，求当时的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某城市随机抽取一年（365天）内100天的空气质量指数API的监测数据，结果统计如下：

    API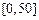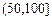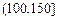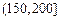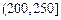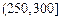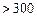
     
     
     
     
     
     
     
     
    空气质量
         		优
         		良
         		轻微污染
         		轻度污染
         		中度污染
         		中度重污染
         		重度污染
     
    天数
         		4
         		13
         		18
         		30
         		9
         		11
         		15
     
     
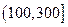    记某企业每天由空气污染造成的经济损失S（单位：元），空气质量指数API为ω。在区间[0，100]对企业没有造成经济损失；在区间对企业造成经济损失成直线模型（当API为150时造成的 经济损失为500元，当API为200时，造成的经济损失为700元）；当API大于300时造成的 经济损失为2000元；
    （1）试写出是S(ω)的表达式;
    （2）试估计在本年内随机抽取一天，该天经济损失S大于200元且不超过600元的概率；
    （3）若本次抽取的样本数据有30天是在供暖季，其中有8天为重度污染，完成下面2×2列联表，并判断能否有95%的把握认为该市本年空气重度污染与供暖有关？
    P(K2 ≥ k0)
         		0.25
         		0.15
         		0.10
         		0.05
         		0.025
         		0.010
         		0.005
         		0.001
     
    k0
         		1.323
         		2.072
         		2.706
         		3.841
         		5.024
         		6.635
         		7.879
         		10.828
     

     

     
    附：

     
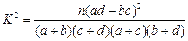
         		非重度污染
         		重度污染
         		合计
     
    供暖季
         		 
         		 
         		 
     
    非供暖季
         		 
         		 
         		 
     
    合计
         		 
         		 
         		100
     
     

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    现有10名教师，其中男教师6名，女教师4名．
    (1)要从中选2名教师去参加会议，有多少种不同的选法？
    (2）现要从中选出4名教师去参加会议，求男、女教师各选2名的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某学校一位教师要去某地参加全国数学优质课比赛，已知他乘火车、轮船、汽车、飞机直接去的概率分别为0.3、0.1、0.2、0.4.
    （1）求他乘火车或乘飞机去的概率；
    （2）他不乘轮船去的概率；

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    “光盘行动”倡导厉行节约，反对铺张浪费，带动大家珍惜粮食，吃光盘子中的食物，得到从中央到民众的支持，为了解某地响应“光盘行动”的实际情况，某校几位同学组成研究性学习小组，从某社区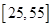岁的人群中随机抽取n人进行了一次调查，得到如下统计表：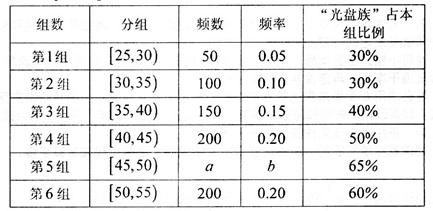

    （1）求a，b的值，并估计本社区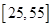岁的人群中“光盘族”所占比例；
    （2）从年龄段在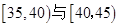的“光盘族”中，采用分层抽样方法抽取8人参加节约粮食宣传活动，并从这8人中选取2人作为领队.
    （1）已知选取2人中1人来自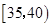中的前提下，求另一人来自年龄段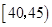中的概率；
    （2）求2名领队的年龄之和的期望值（每个年龄段以中间值计算）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某算法的程序框图如图所示，其中输入的变量x在1,2,3，…，24这24个整数中等可能随机产生．

    (1)分别求出按程序框图正确编程运行时输出y的值为i的概率Pi(i＝1,2,3)；
    (2)甲、乙两同学依据自己对程序框图的理解，各自编写程序重复运行n次后，统计记录了输出y的值为i(i＝1,2,3)的频数．以下是甲、乙所作频数统计表的部分数据．
    甲的频数统计表(部分)

    运行次数n
    		输出y的值
    为1的频数
    		输出y的值
    为2的频数
    		输出y的值
    为3的频数
    30
    		14
    		6
    		10
    …
    		…
    		…
    		…
    2 100
    		1 027
    		376
    		697
     
    乙的频数统计表(部分)
    运行次数n
    		输出y的值
    为1的频数
    		输出y的值
    为2的频数
    		输出y的值
    为3的频数
    30
    		12
    		11
    		7
    …
    		…
    		…
    		…
    2 100
    		1 051
    		696
    		353
     
    当n＝2 100时，根据表中的数据，分别写出甲、乙所编程序各自输出y的值为i(i＝1,2,3)的频率(用分数表示)，并判断两位同学中哪一位所编程序符合算法要求的可能性较大；
    (3)将按程序框图正确编写的程序运行3次，求输出y的值为2的次数ξ的分布列及数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    根据以往的经验，某工程施工期间的降水量X（单位：mm）对工期的影响如下表：

    降水量X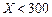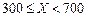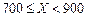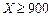




    工期延误天数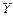
    		0
    		2
    		6
    		10
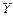    历年气象资料表明，该工程施工期间降水量X小于300，700，900的概率分别为0．3，0．7，0．9．求：
    （1）工期延误天数的均值与方差；（2）在降水量X至少是300的条件下，工期延误不超过6天的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    在0，1，2，3，…，9这十个自然数中，任取三个不同的数字．将取出的三个数字按从小到大的顺序排列，设ξ为三个数字中相邻自然数的组数(例如：若取出的三个数字为0，1，2，则相邻的组为0，1和1，2，此时ξ的值是2)，求随机变量ξ的分布列．

    查看答案和解析>>

    同步练习册答案