
已知曲线f(x)=x2+2x在点(x1,f(x1))处的切线为l.
(Ⅰ)求l的方程;
(Ⅱ)设g(x)=(x+a)f(x),若g(x)在[1,2]上是增函数,求实数a的取值范围;
(Ⅲ)试判断l能否与曲线g(x)=ln(x+1)相切?并说明理由.
科目:高中数学 来源:2004年高考教材全程总复习试卷·数学 题型:044
已知函数f(x)=x(x-a)(x-b),其中0<a<b.
(1)设f(x)在x=s及x=t处取到极值,其中s<t,求证:0<s<a<t<b.
(2)设A(s,f(s)),B(t,f(t)),求证:线段AB的中点C在曲线y=f(x)上.
(3)若a+b<2 ,求证:过原点且与曲线y=f(x)相切的两条直线不可能垂直.
,求证:过原点且与曲线y=f(x)相切的两条直线不可能垂直.
查看答案和解析>>
科目:高中数学 来源:浙江慈溪市2012届高三5月模拟考试数学文科试题 题型:044
已知函数f(x)=x-alnx,(a∈R)
(1)当a=2时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)当x∈[e,e2]是否存在实数a,使得函数f(x)有最大值e,若存在,求出a的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖南省、岳阳县一中高三11月联考理科数学 题型:解答题
(本小题满分13分)(第一问8分,第二问5分)
已知函数f(x)=2lnx,g(x)= ax2+3x.
ax2+3x.
(1)设直线x=1与曲线y=f(x)和y=g(x)分别相交于点P、Q,且曲线y=f(x)和y=g(x)在点P、Q处的切线平行,若方程 f(x2+1)+g(x)=3x+k有四个不同的实根,求实数k的取值范围;
f(x2+1)+g(x)=3x+k有四个不同的实根,求实数k的取值范围;
(2)设函数F(x)满足F(x)+x[f′(x)-g′(x)]=-3x2-(a+6)x+1.其中f′(x),g′(x)分别是函数f(x)与g(x)的导函数;试问是否存在实数a,使得当x∈(0,1]时,F(x)取得最大值,若存在,求出a的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2012届湖南省澧县一中、岳阳县一中高三11月联考理科数学 题型:解答题
(本小题满分13分)(第一问8分,第二问5分)
已知函数f(x)=2lnx,g(x)=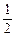 ax2+3x.
ax2+3x.
(1)设直线x=1与曲线y=f(x)和y=g(x)分别相交于点P、Q,且曲线y=f(x)和y=g(x)在点P、Q处的切线平行,若方程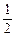 f(x2+1)+g(x)=3x+k有四个不同的实根,求实数k的取值范围;
f(x2+1)+g(x)=3x+k有四个不同的实根,求实数k的取值范围;
(2)设函数F(x)满足F(x)+x[f′(x)-g′(x)]=-3x2-(a+6)x+1.其中f′(x),g′(x)分别是函数f(x)与g(x)的导函数;试问是否存在实数a,使得当x∈(0,1]时,F(x)取得最大值,若存在,求出a的取值范围;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com