
【题目】如图,四棱锥PABCD中,底面ABCD是矩形,PA⊥平面ABCD,AD=1,PA=AB=![]() ,点E是棱PB的中点.
,点E是棱PB的中点.
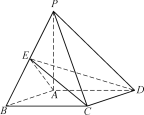
(1)求异面直线EC与PD所成角的余弦值;
(2)求二面角B-EC-D的余弦值.
【答案】(1)![]() .(2.
.(2.![]()
【解析】
(1)先根据题意建立空间直角坐标系,分别求得向量![]() 和向量
和向量![]() 的坐标,再利用线线角的向量方法求解.
的坐标,再利用线线角的向量方法求解.
(2)分别求得平面BEC的一个法向量和平面DEC的一个法向量,再利用面面角向量方法求解,注意根据图形判断二面角与向量夹角的大小关系确定符号.
(1)因为PA⊥底面ABCD,且底面ABCD为矩形,
所以AB,AD,AP两两垂直,
以A为原点,AB,AD,AP分别为x,y,z轴建立空间直角坐标系.
又因为PA=AB=![]() ,AD=1,
,AD=1,
所以A(0,0,0),B ![]() ,C
,C![]() ,D(0,1,0),P
,D(0,1,0),P![]()
因为E是棱PB的中点,所以E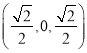 ,
,
所以![]() =
=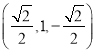 ,
,![]() =(0,1,-
=(0,1,-![]() ),
),
所以cos〈![]() ,
,![]() 〉=
〉=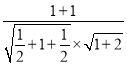 =
=![]() ,
,
所以异面直线EC与PD所成角的余弦值为![]() .
.
(2)由(1)得![]() =
=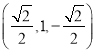 ,
,![]() =(0,1,0),
=(0,1,0),![]() =(
=(![]() ,0,0).
,0,0).
设平面BEC的法向量为![]() =(x1,y1,z1),
=(x1,y1,z1),
所以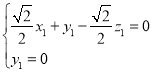
令x1=1,则z1=1,所以平面BEC的一个法向量为![]() =(1,0,1).
=(1,0,1).
设平面DEC的法向量为![]() =(x2,y2,z2),
=(x2,y2,z2),
所以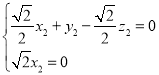
令z2=![]() ,则y2=1,所以平面DEC的一个法向量为
,则y2=1,所以平面DEC的一个法向量为![]() =(0,1,
=(0,1,![]() ),
),
所以cos〈![]() ,
,![]() 〉=
〉=![]() =
=![]()
.由图可知二面角B-EC-D为钝角,所以二面角B-EC-D的余弦值为-![]() .
.


科目:高中数学 来源: 题型:
【题目】下图是函数![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() )在区间
)在区间![]() 上的图象,为了得到这个函数的图象,只需将
上的图象,为了得到这个函数的图象,只需将![]() (
(![]() )的图像上所有的点( )
)的图像上所有的点( )

A. 向左平移![]() 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
B. 向左平移![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的![]() 倍,纵坐标不变
倍,纵坐标不变
C. 向左平移![]() 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
D. 向左平移![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的![]() 倍,纵坐标不变
倍,纵坐标不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】江心洲有一块如图所示的江边,![]() ,
,![]() 为岸边,岸边形成
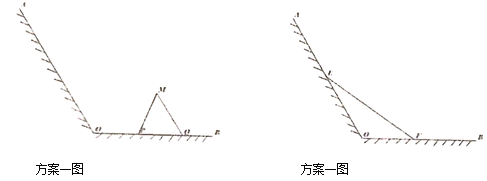
为岸边,岸边形成![]() 角,现拟在此江边用围网建一个江水养殖场,有两个方案:方案l:在岸边
角,现拟在此江边用围网建一个江水养殖场,有两个方案:方案l:在岸边![]() 上取两点
上取两点![]() ,用长度为
,用长度为![]() 的围网依托岸边线
的围网依托岸边线![]() 围成三角形
围成三角形![]() (
(![]() ,
,![]() 两边为围网);方案2:在岸边
两边为围网);方案2:在岸边![]() ,
,![]() 上分别取点
上分别取点![]() ,用长度为
,用长度为![]() 的围网
的围网![]() 依托岸边围成三角形
依托岸边围成三角形![]() .请分别计算
.请分别计算![]() ,
,![]() 面积的最大值,并比较哪个方案好.
面积的最大值,并比较哪个方案好.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了40个用户,根据用户对产品的满意度评分,得到![]() 地区用户满意度评分的频率分布直方图和
地区用户满意度评分的频率分布直方图和![]() 地区用户满意度评分的频数分布表.
地区用户满意度评分的频数分布表.
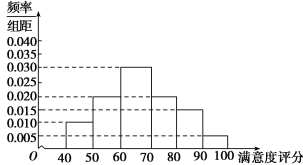
![]() 地区用户满意度评分的频率分布直方图
地区用户满意度评分的频率分布直方图
![]() 地区用户满意度评分的频数分布表
地区用户满意度评分的频数分布表
满意度评分分组 |
|
|
|
|
|
频数 | 2 | 8 | 14 | 10 | 6 |
(1)在图中作出![]() 地区用户满意度评分的频率分布直方图,并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可).
地区用户满意度评分的频率分布直方图,并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可).
![]() 地区用户满意度评分的频率分布直方图
地区用户满意度评分的频率分布直方图
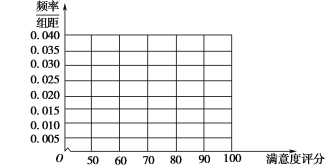
(2)根据用户满意度评分,将用户的满意度分为三个等级:
满意度评分 | 低于70分 | 70分到89分 | td style="width:88.95pt; border-left-style:solid; border-left-width:0.75pt; border-bottom-style:solid; border-bottom-width:0.75pt; padding:3.38pt 5.03pt; vertical-align:middle">|
满意度等级 | 不满意 | 满意 | 非常满意 |
公司负责人为了解用户满意度情况,从![]() 地区中调查8户,其中有2户满意度等级是不满意,求从这8户中随机抽取2户检查,抽到不满意用户的概率.
地区中调查8户,其中有2户满意度等级是不满意,求从这8户中随机抽取2户检查,抽到不满意用户的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
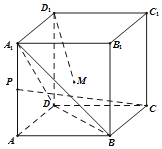
【题目】如图,正方体![]() 的棱长为1,
的棱长为1,![]() 为
为![]() 的中点,
的中点,![]() 在侧面
在侧面![]() 上,有下列四个命题:
上,有下列四个命题:
①若![]() ,则
,则![]() 面积的最小值为
面积的最小值为![]() ;
;
②平面![]() 内存在与
内存在与![]() 平行的直线;
平行的直线;
③过![]() 作平面
作平面![]() ,使得棱
,使得棱![]() ,
,![]() ,
,![]() 在平面
在平面![]() 的正投影的长度相等,则这样的平面
的正投影的长度相等,则这样的平面![]() 有4个;
有4个;
④过![]() 作面
作面![]() 与面
与面![]() 平行,则正方体
平行,则正方体![]() 在面
在面![]() 的正投影面积为
的正投影面积为![]() .
.
则上述四个命题中,真命题的个数为( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分13分)
为回馈顾客,某商场拟通过摸球兑奖的方式对1000位顾客进行奖励,规定:每位顾客从一个装有4个标有面值的球的袋中一次性随机摸出2个球,球上所标的面值之和为该顾客所获的奖励额.
(1)若袋中所装的4个球中有1个所标的面值为50元,其余3个均为10元,求
①顾客所获的奖励额为60元的概率
②顾客所获的奖励额的分布列及数学期望;
(2)商场对奖励总额的预算是60000元,并规定袋中的4个球只能由标有面值10元和50元的两种球组成,或标有面值20元和40元的两种球组成.为了使顾客得到的奖励总额尽可能符合商场的预算且每位顾客所获的奖励额相对均衡,请对袋中的4个球的面值给出一个合适的设计,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在著名的汉诺塔问题中,有三根高度相同的柱子和一些大小及颜色各不相同的圆盘,三根柱子分别为起始柱、辅助柱及目标柱.已知起始柱上套有![]() 个圆盘,较大的圆盘都在较小的圆盘下面.现把圆盘从起始柱全部移到目标柱上,规则如下:每次只能移动一个圆盘,且每次移动后,每根柱上较大的圆盘不能放在较小的圆盘上面,规定一个圆盘从任一根柱上移动到另一根柱上为一次移动.若将
个圆盘,较大的圆盘都在较小的圆盘下面.现把圆盘从起始柱全部移到目标柱上,规则如下:每次只能移动一个圆盘,且每次移动后,每根柱上较大的圆盘不能放在较小的圆盘上面,规定一个圆盘从任一根柱上移动到另一根柱上为一次移动.若将![]() 个圆盘从起始柱移动到目标柱上最少需要移动的次数记为
个圆盘从起始柱移动到目标柱上最少需要移动的次数记为![]() ,则
,则![]() ( )
( )

A. 33B. 31C. 17D. 15
查看答案和解析>>
科目:高中数学 来源: 题型:
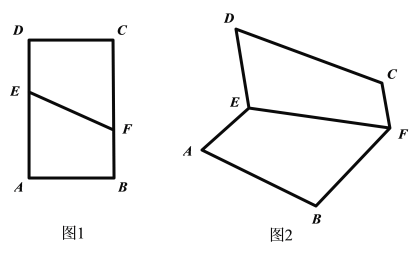
【题目】如图1,直线![]() 将矩形
将矩形![]() 分为两个直角梯形
分为两个直角梯形![]() 和
和![]() ,将梯形
,将梯形![]() 沿边
沿边![]() 翻折,如图2,在翻折过程中(平面
翻折,如图2,在翻折过程中(平面![]() 和平面
和平面![]() 不重合),下列说法正确的是( )
不重合),下列说法正确的是( )
A.存在某一位置,使得![]() 平面
平面![]()
B.存在某一位置,使得![]() 平面
平面![]()
C.存在某一位置,使得![]()
D.在翻折过程中,恒有直线![]() 平面
平面![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com