解:(Ⅰ)f′(x)=-
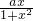
+a=
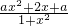
当a=0时,f′(x)=
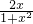
>0?x>0
∴f(x)在(0,+∞)单调递增,在(-∝,0)单调递减.
当a<0且ax
2+2x+a=0的判别式△≤0,
即a≤-1时,f′(x)≤0对x∈R恒成立.
∴f(x)在R上单调递减.
当-1<a<0时,由f′(x)>0得:ax
2+2x+a>0
解得:
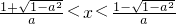
由f′(x)<0可得:x>
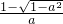
或x<
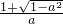
∴f(x)在[
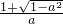
,
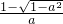
]上单调递增,
在(-∝,
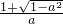
],[
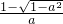
,+∞)上单调递减.
(Ⅱ)由(Ⅰ)当a=-1时,f(x)在(-∞,+∞)上单调递减.
当x>0时f(x)<f(0)
∴ln(1+x
2)-x<0,即ln(1+x
2)<x
∴ln[(1+

)•(1+
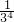
)…(1+
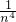
)]
=ln(1+

)•(1+
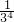
)…(1+
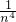
)<

<
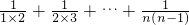
=(1-

)+(

-

)+…+(

)=1-

<1
∴(1+

)•(1+
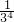
)…(1+
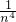
)<e.
分析:(I)先求导数fˊ(x),讨论a的与0和-1的大小,在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0,即可求出函数f(x)的单调区间;
(II)先根据a=-1时,f(x)的单调性得到ln(1+x
2)<x,然后利用该不等式得到ln[(1+

)•(1+
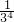
)…(1+
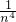
)]<

,最后利用放缩法进行化简,利用裂项法进行求和即可证得结论.
点评:本题主要考查了利用导数研究函数的单调区间,以及分类讨论的数学思想,放缩法和裂项求和法的应用,属于中档题.

 )•(1+
)•(1+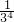 )•…•(1+
)•…•(1+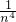 )<e(n∈N*,n≥2,其中无理数e=2.71828…)
)<e(n∈N*,n≥2,其中无理数e=2.71828…)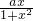 +a=
+a=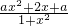
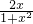 >0?x>0
>0?x>0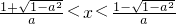
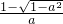 或x<
或x<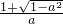
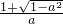 ,
,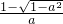 ]上单调递增,
]上单调递增,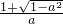 ],[
],[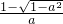 ,+∞)上单调递减.
,+∞)上单调递减. )•(1+
)•(1+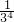 )…(1+
)…(1+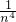 )]
)] )•(1+
)•(1+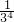 )…(1+
)…(1+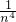 )<
)<
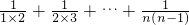 =(1-
=(1- )+(
)+( -
- )+…+(
)+…+( )=1-
)=1- <1
<1 )•(1+
)•(1+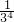 )…(1+
)…(1+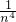 )<e.
)<e. )•(1+
)•(1+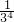 )…(1+
)…(1+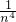 )]<
)]< ,最后利用放缩法进行化简,利用裂项法进行求和即可证得结论.
,最后利用放缩法进行化简,利用裂项法进行求和即可证得结论.

 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案