解:(Ι)若a=1,集合A中的不等式为:x
2-4x+3≤0,
因式分解得:(x-1)(x-3)≤0,
可化为:
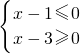
或
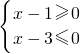
,
解得:1≤x≤3,
∴集合A={x|1≤x≤3},
由集合B中的不等式
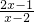
≤0,
可化为:(2x-1)(x-2)≤0,且x-2≠0,
变形为:
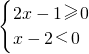
或
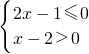
,
解得:

≤x<2,
∴集合B={x|

≤x<2},
则A∩B={x|1<x<2};
(ΙΙ)集合A中的不等式x
2-2(a+1)x+a(a+2)≤0,
分解因式得:(x-a)(x-a-2)≤0,
∵a<a+2,∴a≤x≤a+2,
由第一问得到集合B={x|

≤x<2},
又A∩B=∅,
∴a+2<

或a≥2,
则a的取值范围为a<-

或a≥2.
分析:(Ι)把a=1代入集合A中的不等式中确定出一元二次不等式,将不等式左边分解因式后,根据两数相乘积为负数,两因式异号转化为两个不等式组,求出不等式组的解集即可得到原不等式的解集,确定出集合A,集合B中的不等式根据两数相除商为负数,得到被除式与除式异号,转化为两个不等式组,求出不等式组的解集得到原不等式的解集,确定出集合B,找出两集合的公共部分,即可求出两集合的交集;
(ΙΙ)把集合A中的不等式分解因式后,根据a小于a+2,表示出不等式的解集,确定出集合A,由第一问求出的集合B,根据两集合的交集为空集,列出关于a的不等式,求出不等式的解集,即可得到a的取值范围.
点评:此题考查了交集及其运算,涉及的知识有:一元二次不等式的解法,其他不等式的解法,以及集合中参数的取值问题,利用了转化的思想,是高考中常考的基本题型.

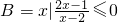
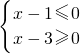 或
或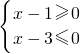 ,
,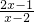 ≤0,
≤0,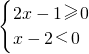 或
或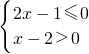 ,
, ≤x<2,
≤x<2, ≤x<2},
≤x<2}, ≤x<2},
≤x<2}, 或a≥2,
或a≥2, 或a≥2.
或a≥2.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案