练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．某商店每双皮鞋的进货价为80元，根据以往经验，以每双90元销售时，每月能卖出400双，而每加价1元或减价1元销售时，每月销量会减少或增加20双，为了每月获取最大利润，商店应如何定价？每月的最大利润为多少？

    分析 假设售价在90元的基础上涨x元，从而得到销售量，进而可以构建函数关系式，利用二次函数求最值的方法求出函数的最值．

    解答 解：设售价在90元的基础上涨或减价x元，因为这种商品每个涨价或减价1元，其销售量就减少或增加20个，所以若涨或减价x元，则销售量减少或增加20x
    则按90+x元售出时，能售出400-20x个，每个的利润是90+x-80=10+x元
    设总利润为y元，则y=（10+x）（400-20x）=-20x2+200x+4000，对称轴为x=5，定义域为（0≤x＜20），
    所以x=5时，y有最大值，售价则为95元，
    所以售价定为每个95元时，利润最大，每月的最大利润为4500元．

    点评 本题以实际问题为载体，考查函数模型的构建，考查利用数学知识解决实际问题，解题的关键是构造利润函数．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    14．利用“长方体ABCD-A1B1C1D1中，四面体A1BC1D”的特点，求得四面体PMNR（其中PM=NR=$\sqrt{10}$，PN=MR=$\sqrt{13}$，MN=PR=$\sqrt{5}$）的外接球的表面积为（　　）
    A．14πB．16πC．13πD．15π

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．设函数$f（x）=sin（2x-\frac{π}{2}），x∈R$，则f（x）是（　　）
    A．最小正周期为π的奇函数B．最小正周期为$\frac{π}{2}$的偶函数
    C．最小正周期为$\frac{π}{2}$的奇函数D．最小正周期为π的偶函数

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．求下列表达式的值
    （1）$\frac{（{a}^{\frac{2}{3}}•{b}^{-1}）^{-\frac{1}{2}}•{a}^{\frac{1}{2}}•{b}^{\frac{1}{3}}}{\root{6}{a•{b}^{5}}}$（a＞0，b＞0）
    （2）$\frac{1}{2}$lg$\frac{32}{49}$-$\frac{4}{3}$lg$\sqrt{8}$+lg$\sqrt{245}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

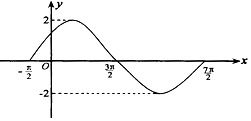    19．已知f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，0＜φ＜π）在一个周期内图象如图所示．
    （1）试确定A，ω，φ的值．
    （2）求y=$\sqrt{3}$与函数f（x）的交点坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

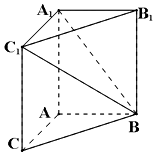    9．如图，在三棱柱ABC-A1B1C1中，AA1C1C是边长为的正方形，平面ABC⊥平面AA1C1C，AB=3，BC=5．
    （1）求证：AA1⊥平面ABC；
    （2）求二面角A1-BC1-B1的余弦值；
    （3）在线段BC1上是否存在点D，使得AD⊥A1B？若存在，求出$\frac{BD}{B{C}_{1}}$的值，若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知函数f（x）=$\frac{1-x}{ax}$+lnx，且a＞0
    （1）若函数f（x）在[1，+∞）上是增函数，求a的取值范围；
    （2）当a=1时，求函数f（x）在[1，e]的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知函数$f（x）=\sqrt{-{x^2}+2x+8}$的定义域为集合A，函数g（x）=lg（-x2+6x+m）的定义域为集合B．
    （1）当m=-5时，求A∩∁UB；
    （2）若A∩B={x|-1＜x≤4}，求实数m的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知，△ABC中，A（1，1），B（2，-3），C（3，5），写出满足下列条件的直线方程（要求最终结果都用直线的一般式方程表示，其他形式的结果不得分．）
    （1）求直线AB方程；
    （2）BC边中点D，求中线AD方程；
    （3）BC边上的高线的方程；
    （4）BC边的垂直平分线的方程．

    查看答案和解析>>

    同步练习册答案