
【题目】北京市为了缓解交通压力,计划在某路段实施“交通限行”,为调查公众对该路段“交通限行”的态度,某机构从经过该路段的人员中随机抽查了80人进行调查,将调查情况进行整理,制成下表:
年龄(岁) |
|
|
|
|
人数 | 24 | 26 | 16 | 14 |
赞成人数 | 12 | 14 |
| 3 |
(1)若经过该路段的人员对“交通限行”的赞成率为0.40,求![]() 的值;
的值;
(2)在(1)的条件下,若从年龄在![]() ,
,![]() 内的两组赞成“交通限行”的人中在随机选取2人进行进一步的采访,求选中的2人中至少有1人来自
内的两组赞成“交通限行”的人中在随机选取2人进行进一步的采访,求选中的2人中至少有1人来自![]() 内的概率.
内的概率.
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:
【题目】在一次“知识竞赛”活动中,有![]() 四道题,其中
四道题,其中![]() 为难度相同的容易题,
为难度相同的容易题, ![]() 为中档题,
为中档题, ![]() 为较难题,现甲、乙两位同学均需从四道题目中随机抽取一题作答.
为较难题,现甲、乙两位同学均需从四道题目中随机抽取一题作答.
(1)求甲、乙两位同学所选的题目难度相同的概率;
(2)求甲所选题目的难度大于乙所选题目的难度的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某志愿者到某山区小学支教,为了解留守儿童的幸福感,该志愿者对某班40名学生进行了一次幸福指数的调查问卷,并用茎叶图表示如下(注:图中幸福指数低于70,说明孩子幸福感弱;幸福指数不低于70,说明孩子幸福感强).
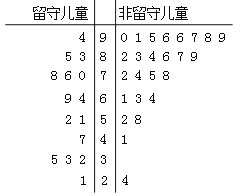
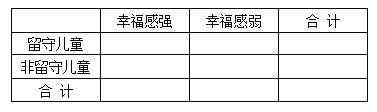
(Ⅰ)根据茎叶图中的数据完成![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为孩子的幸福感强与是否是留守儿童有关?
的把握认为孩子的幸福感强与是否是留守儿童有关?
(Ⅱ)从15个留守儿童中按幸福感强弱进行分层抽样,共抽取5人,又在这5人中随机抽取2人进行家访,求这2个学生中恰有一人幸福感强的概率.
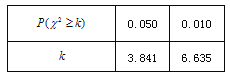
参考公式: 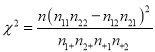 ; 附表:
; 附表:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业共有20条生产线,由于受生产能力和技术水平等因素的影响,会产生一定量的次品.根据经验知道,每台机器产生的次品数![]() 万件与每台机器的日产量
万件与每台机器的日产量![]() 万件
万件![]() 之间满足关系:
之间满足关系: ![]() .已知每生产1万件合格的产品可以以盈利3万元,但每生产1万件次品将亏损1万元.
.已知每生产1万件合格的产品可以以盈利3万元,但每生产1万件次品将亏损1万元.
(Ⅰ)试将该企业每天生产这种产品所获得的利润![]() 表示为
表示为![]() 的函数;
的函数;
(Ⅱ)当每台机器的日产量为多少时,该企业的利润最大,最大为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某玩具生产公司每天计划生产卫兵、骑兵、伞兵这三种玩具共100个,生产一个卫兵需5分钟,生产一个骑兵需7分钟,生产一个伞兵需4分钟,已知总生产时间不超过10小时,若生产一个卫兵可获利润5元,生产一个骑兵可获利润6元,生产一个伞兵可获利润3元.
(1)用每天生产的卫兵个数![]() 与骑兵个数
与骑兵个数![]() 表示每天的利润
表示每天的利润![]() (元);
(元);
(2)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com