
已知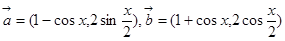 ,
,
设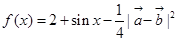 .
.
(Ⅰ)求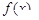 的表达式;
的表达式;
(Ⅱ)若函数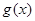 和函数
和函数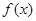 的图象关于原点对称,
的图象关于原点对称,
(ⅰ)求函数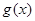 的解析式;
的解析式;
(ⅱ)若函数 在区间
在区间 上是增函数,求实数l的取值范围.
上是增函数,求实数l的取值范围.
Ⅰ)
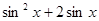 ;(Ⅱ)函数
;(Ⅱ)函数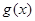 的解析式为
的解析式为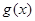 =
-sin2x+2sinx ;
=
-sin2x+2sinx ;
(Ⅲ) 。
。
【解析】
试题分析:(Ⅰ)
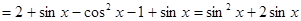 4分
4分
(Ⅱ)设函数 的图象上任一点
的图象上任一点 关于原点的对称点为
关于原点的对称点为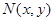
则 ,
.5分
,
.5分
∵点 在函数
在函数 的图象上
的图象上
 ,即
,即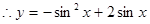
∴函数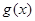 的解析式为
的解析式为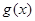 =
-sin2x+2sinx 7分
=
-sin2x+2sinx 7分
(Ⅲ)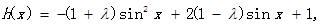
设 9分
9分
则有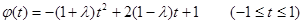
当 时,
时, (t)=4t+1在[-1,1]上是增函数,∴λ=
-1 11分
(t)=4t+1在[-1,1]上是增函数,∴λ=
-1 11分
当 时,对称轴方程为直线
时,对称轴方程为直线 .
.
ⅰ) 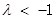 时,
时, ,解得
,解得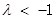
ⅱ)当 时,
时, ,解得
,解得
综上: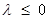 .
.
 实数l的取值范围为
实数l的取值范围为 14分
14分
考点:本题主要考查平面向量的坐标运算,三角函数和差倍半公式的应用,二次函数图象和性质。
点评:典型题,为研究三角函数的图象和性质,往往需要将函数“化一”,这是常考题型。首先运用“三角公式”进行化简,为进一步解题奠定了基础。(3)小题利用“换元思想”,转化成二次函数在闭区间的单调性研究问题,根据图象对称轴受到的限制,求得实数l的取值范围。


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案科目:高中数学 来源: 题型:
| 1 |
| x |
| 2 |
| y |
| 1 |
| x |
| 2 |
| y |
| π |
| 2 |
| 2 |
| tan2α |
| 2 |
| 2 |
| tan2α |
| 2 |
| 2 |
| 2 |
| 1-x |
| x |
| x+1 |
| x |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省高三第一次统练文科数学试卷(解析版) 题型:解答题
在极坐标系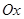 中,已知曲线
中,已知曲线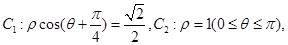
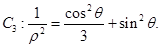 设
设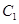 与
与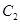 交于点
交于点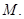
(I)求点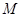 的极坐标;
的极坐标;
(II)若动直线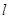 过点
过点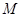 ,且与曲线
,且与曲线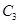 交于两个不同的点
交于两个不同的点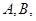 求
求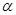
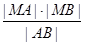 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源:2013届江苏省度高二下期中文科数学试卷(解析版) 题型:解答题
(14分)已知 ,设命题
,设命题 函数
函数 在R上单调递增;命题
在R上单调递增;命题 不等式
不等式 对任意
对任意 恒成立。若
恒成立。若 且
且 为假,
为假, 或
或 为真,求
为真,求 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com