
【题目】已知函数y=f(x)是定义域为R的偶函数. 当x≥0时,f(x)= 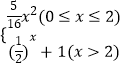 ,若关于x的方程[f(x)]2+af(x)+b=0,a,b∈R有且仅有6个不同实数根,则实数a的取值范围是 .
,若关于x的方程[f(x)]2+af(x)+b=0,a,b∈R有且仅有6个不同实数根,则实数a的取值范围是 .
【答案】(﹣ ![]() ,﹣
,﹣ ![]() )∪(﹣
)∪(﹣ ![]() ,﹣1)
,﹣1)
【解析】解:依题意f(x)在(﹣∞,﹣2)和(0,2)上递增,在(﹣2,0)和(2,+∞)上递减,
当x=±2时,函数取得极大值 ![]() ;
;
当x=0时,取得极小值0.
要使关于x的方程[f(x)]2+af(x)+b=0,a,b∈R有且只有6个不同实数根,
设t=f(x),
则t2+at+b=0必有两个根t1、t2 ,
则有两种情况符合题意:
1)t1= ![]() ,且t2∈(1,
,且t2∈(1, ![]() ),
),
此时﹣a=t1+t2 ,
则a∈(﹣ ![]() ,﹣
,﹣ ![]() );
);
2)t1∈(0,1],t2∈(1, ![]() ),
),
此时同理可得a∈(﹣ ![]() ,﹣1),
,﹣1),
综上可得a的范围是(﹣ ![]() ,﹣
,﹣ ![]() )∪(﹣
)∪(﹣ ![]() ,﹣1).
,﹣1).
所以答案是:(﹣ ![]() ,﹣
,﹣ ![]() )∪(﹣
)∪(﹣ ![]() ,﹣1).
,﹣1).


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年![]() 位居民每人的月均用水量(单位:吨),将数据按照
位居民每人的月均用水量(单位:吨),将数据按照![]() 分成
分成![]() 组,制成了如图所示的频率分布直方图.
组,制成了如图所示的频率分布直方图.
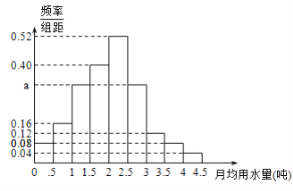
(1)求直方图中的![]() 值;
值;
(2)设该市有![]() 万居民,估计全市居民中月均用水量不低于
万居民,估计全市居民中月均用水量不低于![]() 吨的人数.说明理由;
吨的人数.说明理由;
(3)估计居民月均用水量的中位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知直线2x﹣y﹣1=0与直线x﹣2y+1=0交于点P.
(Ⅰ)求过点P且平行于直线3x+4y﹣15=0的直线![]() 的方程;(结果写成直线方程的一般式)
的方程;(结果写成直线方程的一般式)
(Ⅱ)求过点P并且在两坐标轴上截距相等的直线![]() 方程(结果写成直线方程的一般式)
方程(结果写成直线方程的一般式)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)当a<0时,若x>0,使f(x)≤0成立,求a的取值范围;
(2)令g(x)=f(x)﹣(a+1)x,a∈(1,e],证明:对x1 , x2∈[1,a],恒有|g(x1)﹣g(x2)|<1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,河的两岸,分别有生活小区ABC和DEF,其中AB⊥BC,EF⊥DF,DF⊥AB,C,E,F三点共线,FD与BA的延长线交于点O,测得AB=3km,BC=4km,DF= ![]() km,FE=3km,EC=
km,FE=3km,EC= ![]() km.若以OA,OD所在直线为x,y轴建立平面直角坐标系xoy,则河岸DE可看成是曲线y=
km.若以OA,OD所在直线为x,y轴建立平面直角坐标系xoy,则河岸DE可看成是曲线y= ![]() (其中a,b为常数)的一部分,河岸AC可看成是直线y=kx+m(其中k,m为常数)的一部分.
(其中a,b为常数)的一部分,河岸AC可看成是直线y=kx+m(其中k,m为常数)的一部分. 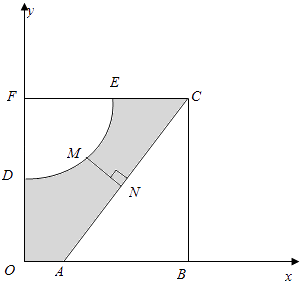
(1)求a,b,k,m的值;
(2)现准备建一座桥MN,其中M,N分别在DE,AC上,且MN⊥AC,设点M的横坐标为t.
①请写出桥MN的长l关于t的函数关系式l=f(t),并注明定义域;
②当t为何值时,l取得最小值?最小值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=x2lnx,g(x)=ax3﹣x2 .
(1)求函数f(x)的最小值;
(2)若存在x∈(0,+∞),使f(x)>g(x),求实数a的取值范围;
(3)若使方程f(x)﹣g(x)=0在x∈[ ![]() ,en](其中e=2.7…为自然对数的底数)上有解的最小a的值为an , 数列{an}的前n项和为Sn , 求证:Sn<3.
,en](其中e=2.7…为自然对数的底数)上有解的最小a的值为an , 数列{an}的前n项和为Sn , 求证:Sn<3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx﹣ax﹣3(a≠0).
(1)讨论f(x)的单调性;
(2)若f(x)+(a+1)x+4﹣e≤0对任意x∈[e,e2]恒成立,求实数a的取值范围(e为自然常数);
(3)求证ln(22+1)+ln(32+1)+ln(42+1)+…+ln(n2+1)<1+2lnn!(n≥2,n∈N*)(n!=1×2×3×…×n).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com