
 可把平面直角坐标系上的点P(x,y)变换到这一平面上的点P′(x′,y′).特别地,若曲线M上一点P经变换公式T变换后得到的点P'与点P重合,则称点P是曲线M在变换T下的不动点.
可把平面直角坐标系上的点P(x,y)变换到这一平面上的点P′(x′,y′).特别地,若曲线M上一点P经变换公式T变换后得到的点P'与点P重合,则称点P是曲线M在变换T下的不动点. ,长轴顶点和短轴顶点间的距离为2.求该椭圆C的标准方程.并求出当
,长轴顶点和短轴顶点间的距离为2.求该椭圆C的标准方程.并求出当 时,其两个焦点F1、F2经变换公式T变换后得到的点F1′和F2′的坐标;
时,其两个焦点F1、F2经变换公式T变换后得到的点F1′和F2′的坐标; 时,求(1)中的椭圆C在变换T下的所有不动点的坐标;
时,求(1)中的椭圆C在变换T下的所有不动点的坐标; (
( ,k∈Z)下的不动点的存在情况和个数.
,k∈Z)下的不动点的存在情况和个数.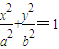 (a>b>0),求出c,a,b然后结合定义变换T,求出点F1′和F2′的坐标.
(a>b>0),求出c,a,b然后结合定义变换T,求出点F1′和F2′的坐标.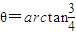 时,利用(1)中的椭圆C在变换T下,点P(x,y)∈C,根据椭圆方程求出的不动点的坐标;
时,利用(1)中的椭圆C在变换T下,点P(x,y)∈C,根据椭圆方程求出的不动点的坐标;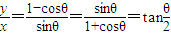 ,设双曲线方程为
,设双曲线方程为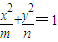 (mn<0),
(mn<0),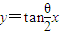 代入,推出
代入,推出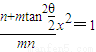 讨论mn<0,故当
讨论mn<0,故当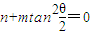 时,方程
时,方程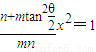 无解;
无解;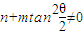 时,要使不动点存在,则需
时,要使不动点存在,则需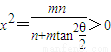 ,
,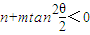 时,双曲线在变换T下一定有2个不动点,否则不存在不动点.
时,双曲线在变换T下一定有2个不动点,否则不存在不动点.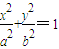 (a>b>0),
(a>b>0),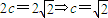 ,即a2-b2=2①.
,即a2-b2=2①.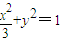 .
.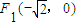 和
和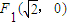 .
.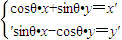 ,当
,当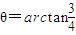 时,
时,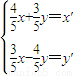
 和
和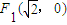 的坐标由变换公式T变换得到.于是,
的坐标由变换公式T变换得到.于是,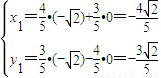 ,即F1′的坐标为
,即F1′的坐标为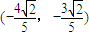 ;
;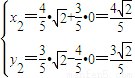 即F2′的坐标为
即F2′的坐标为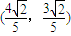 .
.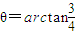 时,
时,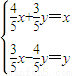 ⇒x=3y,由点P(x,y)∈C,即P(3y,y)∈C,
⇒x=3y,由点P(x,y)∈C,即P(3y,y)∈C,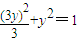
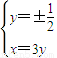 ,因而椭圆
,因而椭圆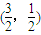 和
和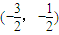 .
.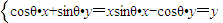 ⇒
⇒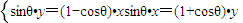
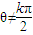 ,k∈Z,故
,k∈Z,故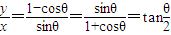 .
.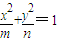 (mn<0),由
(mn<0),由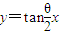 代入得
代入得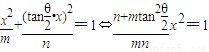 ,
,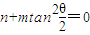 时,方程
时,方程 无解;
无解;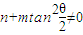 时,要使不动点存在,则需
时,要使不动点存在,则需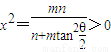 ,
,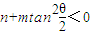 时,双曲线在变换T下一定有2个不动点,否则不存在不动点.
时,双曲线在变换T下一定有2个不动点,否则不存在不动点.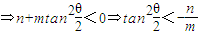 ;
;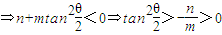 .
.

 名师点拨卷系列答案
名师点拨卷系列答案科目:高中数学 来源: 题型:
|
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
|
| kπ |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com