
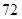 万元建起一座汽车零件加工厂,第一年各种经费
万元建起一座汽车零件加工厂,第一年各种经费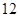 万元,以后每年增加
万元,以后每年增加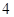 万元,每年的产品销售收入
万元,每年的产品销售收入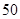 万元.
万元.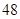 万元出售该厂;
万元出售该厂;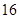 万元出售该厂.
万元出售该厂. 年起;(2)两种方案获利都是
年起;(2)两种方案获利都是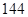 万元,但方案①只需要
万元,但方案①只需要 年,而方案②需要
年,而方案②需要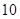 年,所以选择方案①最合算.
年,所以选择方案①最合算. 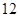 为首项、
为首项、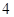 为公差的等差数列,设纯利润与年数的关系为
为公差的等差数列,设纯利润与年数的关系为 ,则
,则 . ………………3分
. ………………3分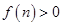 ,即
,即 ,解得
,解得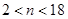 .
.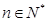 可知,该工厂从第
可知,该工厂从第 年起开始获得纯利润; …………………………5分
年起开始获得纯利润; …………………………5分 ,当且仅当
,当且仅当 ,即
,即 时取等号,故按方案①共获利
时取等号,故按方案①共获利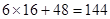 万元,此时
万元,此时 ; ………………………………8分
; ………………………………8分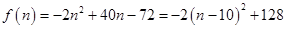 ,当
,当 时,
时,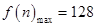 ,故按方案②共获利
,故按方案②共获利 万元,此时
万元,此时 .
.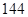 万元,但方案①只需要
万元,但方案①只需要 年,而方案②需要
年,而方案②需要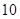 年,所以选择方案①最合算. ………………………………12分
年,所以选择方案①最合算. ………………………………12分

科目:高中数学 来源:不详 题型:单选题
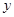 随自变量
随自变量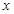 变化的一组数据,由此可判断它最可能的函数模型为
变化的一组数据,由此可判断它最可能的函数模型为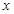 |  |  | 0 | 1 | 2 | 3 |
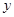 |  |  | 1 | 4 | 16 | 64 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
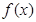 的定义域为
的定义域为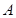 ,若存在非零实数
,若存在非零实数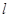 使得对于任意
使得对于任意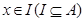 ,有
,有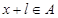 ,且
,且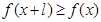 ,则称
,则称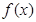 为
为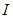 上的
上的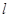 高调函数,如果定义域为
高调函数,如果定义域为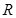 的函数
的函数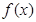 是奇函数,当
是奇函数,当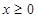 时,
时,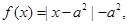 且函数
且函数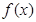 为
为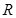 上的1高调函数,那么实数
上的1高调函数,那么实数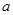 的取值范围为( )
的取值范围为( )A.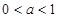 | B.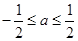 | C.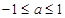 | D.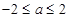 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com