
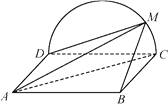
【题目】如图,边长为2的正方形![]() 所在的平面与半圆弧
所在的平面与半圆弧![]() 所在平面垂直,
所在平面垂直,![]() 是
是![]() 上异于
上异于![]() ,
,![]() 的点.
的点.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)当三棱锥![]() 体积最大时,求面
体积最大时,求面![]() 与面
与面![]() 所成二面角的正弦值.
所成二面角的正弦值.
【答案】(1)见解析
(2)![]()
【解析】分析:(1)先证![]() 平面CMD,得
平面CMD,得![]() ,再证
,再证![]() ,进而完成证明。
,进而完成证明。
(2)先建立空间直角坐标系,然后判断出![]() 的位置,求出平面
的位置,求出平面![]() 和平面
和平面![]() 的法向量,进而求得平面
的法向量,进而求得平面![]() 与平面
与平面![]() 所成二面角的正弦值。
所成二面角的正弦值。
详解:(1)由题设知,平面CMD⊥平面ABCD,交线为CD.因为BC⊥CD,BC![]() 平面ABCD,所以BC⊥平面CMD,故BC⊥DM.
平面ABCD,所以BC⊥平面CMD,故BC⊥DM.
因为M为![]() 上异于C,D的点,且DC为直径,所以 DM⊥CM.
上异于C,D的点,且DC为直径,所以 DM⊥CM.
又 BC![]() CM=C,所以DM⊥平面BMC.
CM=C,所以DM⊥平面BMC.
而DM![]() 平面AMD,故平面AMD⊥平面BMC.
平面AMD,故平面AMD⊥平面BMC.
(2)以D为坐标原点,![]() 的方向为x轴正方向,建立如图所示的空间直角坐标系Dxyz.
的方向为x轴正方向,建立如图所示的空间直角坐标系Dxyz.
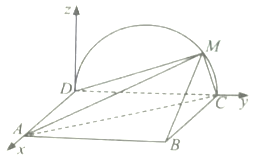
当三棱锥MABC体积最大时,M为![]() 的中点.
的中点.
由题设得![]() ,
,
![]()
设![]() 是平面MAB的法向量,则
是平面MAB的法向量,则
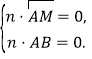 即
即![]()
可取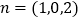 .
.
![]() 是平面MCD的法向量,因此
是平面MCD的法向量,因此
![]() ,
,
![]() ,
,
所以面MAB与面MCD所成二面角的正弦值是![]() .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l经过点A(﹣1,0),其倾斜角是α,以原点O为极点,以x轴的非负半轴为极轴,与直角坐标系xOy取相同的长度单位,建立极坐标系.设曲线C的极坐标方程是ρ2=6ρcosθ﹣5.
(Ⅰ)若直线l和曲线C有公共点,求倾斜角α的取值范围;
(Ⅱ)设B(x,y)为曲线C任意一点,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,A、B、C为⊙O上三点,B为 ![]() 的中点,P为AC延长线上一点,PQ与⊙O相切于点Q,BQ与AC相交于点D.
的中点,P为AC延长线上一点,PQ与⊙O相切于点Q,BQ与AC相交于点D.
(Ⅰ)证明:△DPQ为等腰三角形;
(Ⅱ)若PC=1,AD=PD,求BDQD的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,PA⊥平面ABCD,四边形ABCD为梯形,AD∥BC,BC=6,PA=AD=CD=2,E为BC上一点且BE= ![]() BC,PB⊥AE.
BC,PB⊥AE. 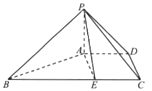
(1)求证:AB⊥PE;
(2)求二面角B﹣PC﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由无理数引发的数学危机一直延续到19世纪.直到1872年,德国数学家戴德金从连续性的要求出发,用有理数的“分割”来定义无理数(史称戴德金分割),并把实数理论建立在严格的科学基础上,才结束了无理数被认为“无理”的时代,也结束了持续2000多年的数学史上的第一次大危机.所谓戴德金分割,是指将有理数集![]() 划分为两个非空的子集
划分为两个非空的子集![]() 与
与![]() ,且满足
,且满足![]() ,
,![]() ,
,![]() 中的每一个元素都小于
中的每一个元素都小于![]() 中的每一个元素,则称
中的每一个元素,则称![]() 为戴德金分割.试判断,对于任一戴德金分割
为戴德金分割.试判断,对于任一戴德金分割![]() ,下列选项中,不可能成立的是( )
,下列选项中,不可能成立的是( )
A. ![]() 没有最大元素,
没有最大元素, ![]() 有一个最小元素 B.
有一个最小元素 B. ![]() 没有最大元素,
没有最大元素, ![]() 也没有最小元素
也没有最小元素
C. ![]() 有一个最大元素,
有一个最大元素, ![]() 有一个最小元素 D.
有一个最小元素 D. ![]() 有一个最大元素,
有一个最大元素, ![]() 没有最小元素
没有最小元素
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com