给定数列

(1)判断

是否为有理数,证明你的结论;
(2)是否存在常数

.使

对

都成立? 若存在,找出

的一个值, 并加以证明; 若不存在,说明理由.
(1)

是无理数 (2)

(或

等).则对

,均有

成立.证明略.
试题分析:(1) 设

是无理数, 利用反证法推出矛盾即可;(2)先设

然后得到

,用放缩法证出


,再借助错位相减法得

<3,即对

,均有

成立.
解:(1)

是无理数, 若不然,设

.
则

即

必为有理数,这与

是无理数矛盾.
(2)设

则

.
于是

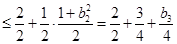






令

.
则

.
从而可取

(或

等).则对

,
均有

成立.
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
已知数列
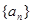
满足
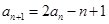
(
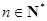
).
(1)若数列
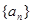
是等差数列,求数列
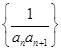
的前
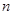
项和
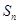
;
(2)证明:数列
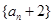
不可能是等比数列.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知数列{a
n},{b
n}都是公差为1的等差数列,其首项分别为a
1,b
1,且a
1+b
1=5,a
1,b
1∈N
*.设c
n=ab
n(n∈N
*),则数列{c
n}的前10项和等于( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
已知各项均为正数的等差数列
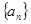
的前10项和为100,那么
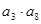
的最大值为
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
等差数列
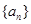
的前n项和为
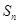
,已知
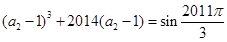
,
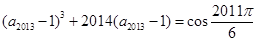
,则
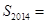
( )
| A.2014 | B.4028 | C.0 | D. [ [ |
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
数列

的前

项和为

,

,
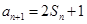
,等差数列

满足

,

.
(1)求数列

,数列

的通项公式;
(2)若对任意的

,不等式

恒成立,求实数

的取值范围.
查看答案和解析>>


 是否为有理数,证明你的结论;
是否为有理数,证明你的结论; .使
.使 对
对 都成立? 若存在,找出
都成立? 若存在,找出 的一个值, 并加以证明; 若不存在,说明理由.
的一个值, 并加以证明; 若不存在,说明理由. 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案