
由命题“存在x∈R,使e|x-1|-m≤0”是假命题,得m的取值范围是(-∞,a),则实数a的取值是( )
| A.(-∞,1) | B.(-∞,2) | C.1 | D.2 |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:单选题
下列说法正确的是( )
A.“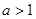 ”是“ ”是“ 上为增函数”的充要条件 上为增函数”的充要条件 |
B.命题“ 使得 使得 ”的否定是:“ ”的否定是:“  ” ” |
C.“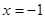 ”是“ ”是“ ”的必要不充分条件 ”的必要不充分条件 |
D.命题p:“ ”,则Øp是真命题 ”,则Øp是真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
给定下列四个命题:
①若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;
②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;
③垂直于同一直线的两条直线相互平行;
④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.
其中,为真命题的是( )
| A.①和② | B.②和③ | C.③和④ | D.②和④ |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
下列关于命题的说法正确的是
A.命题“若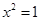 ,则 ,则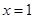 ”的否命题为:”若 ”的否命题为:”若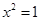 ,则 ,则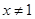 ” ” |
B.“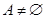 ”是“ ”是“ 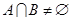 ”的充分不必要条件 ”的充分不必要条件 |
C.命题“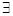 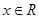 ,使得 ,使得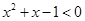 ”的否定是“ ”的否定是“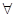 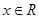 ,均有 ,均有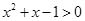 ” ” |
D.命题“若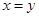 ,则 ,则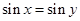 ”的逆否命题为真命题 ”的逆否命题为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
如果a,b,c都是实数,那么P:ac<0,是q:关于x的方程ax2+bx+c=0有一个正根和一个负根的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
设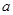 ,
,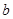 ,
,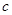 是空间三条直线,
是空间三条直线,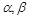 是空间两个平面,则下列命题中,逆命题不成立
是空间两个平面,则下列命题中,逆命题不成立
的是 ( )
A.当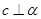 时,若 时,若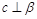 ,则 ,则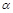 ∥ ∥ |
B.当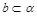 时,若 时,若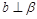 ,则 ,则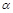 ⊥ ⊥ |
C.当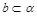 ,且c是a在 ,且c是a在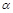 内的射影时,若 内的射影时,若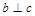 ,则 ,则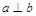 |
D.当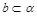 ,且 ,且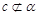 时, 时,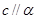 ,则 ,则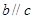 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com