
【题目】已知椭圆![]() :
:![]() 经过点
经过点![]() (
(![]() ,
,![]() ),且两个焦点
),且两个焦点![]() ,
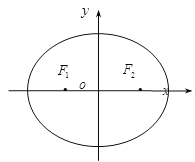
,![]() 的坐标依次为(
的坐标依次为(![]() 1,0)和(1,0).
1,0)和(1,0).
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)设![]() ,
,![]() 是椭圆
是椭圆![]() 上的两个动点,
上的两个动点,![]() 为坐标原点,直线
为坐标原点,直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,求当
,求当![]() 为何值时,直线
为何值时,直线![]() 与以原点为圆心的定圆相切,并写出此定圆的标准方程.
与以原点为圆心的定圆相切,并写出此定圆的标准方程.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】双曲线的方程是![]() -y2=1.
-y2=1.
(1)直线l的倾斜角为![]() ,被双曲线截得的弦长为
,被双曲线截得的弦长为![]() ,求直线l的方程;
,求直线l的方程;
(2)过点P(3,1)作直线l′,使其被双曲线截得的弦恰被P点平分,求直线l′的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游景点有50辆自行车供游客租赁使用,管理这些自行车的费用是每日115元。根据经验,若每辆自行车的日租金不超过6元,则自行车可以全部租出;若超过6元,则每提高1元,租不出去的自行车就增加3辆.规定:每辆自行车的日租金不超过20元,每辆自行车的日租金![]() 元只取整数,并要求出租所有自行车一日的总收入必须超过一日的管理费用,用
元只取整数,并要求出租所有自行车一日的总收入必须超过一日的管理费用,用![]() 表示出租所有自行车的日净收入(即一日中出租所以自行车的总收入减去管理费用后的所得).
表示出租所有自行车的日净收入(即一日中出租所以自行车的总收入减去管理费用后的所得).
(1)求函数![]() 的解析式及定义域;
的解析式及定义域;
(2)试问日净收入最多时每辆自行车的日租金应定为多少元?日净收入最多为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】央视人民网报道:2019年7月15日,平顶山市文物管理局有关人士表示,郏县北大街古墓群抢救性发掘工作结束,共发现古墓539座,已发掘墓葬93座。该墓地是一处大型古墓群,在已发掘的93座墓葬中,有战国时期墓葬32座、两汉时期墓葬56座、唐墓2座、宋墓3座。生物体死亡后,它机体内原有的碳14会按确定的规律衰减,大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”.检测一墓葬女尸出土时碳14的残余量约占原始含量的79%,则可推断为该墓葬属于( )时期(辅助数据:![]() )
)
参考时间轴:

A.战国B.两汉C.唐朝D.宋朝
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①如果平面![]() 外一条直线
外一条直线![]() 与平面
与平面![]() 内一条直线
内一条直线![]() 平行,那么
平行,那么![]() ;
;
②过空间一定点有且只有一条直线与已知平面垂直;
③如果一条直线垂直于一个平面内的无数条直线,那么这条直线与这个平面垂直;
④若两个相交平面都垂直于第三个平面,则这两个平面的交线垂直于第三个平面.
其中真命题的个数为
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以平面直角坐标系
为参数),以平面直角坐标系![]() 的原点
的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的直角坐标方程及曲线
的直角坐标方程及曲线![]() 上的动点
上的动点![]() 到坐标原点
到坐标原点![]() 的距离
的距离![]() 的最大值;
的最大值;
(Ⅱ)若曲线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,且与
两点,且与![]() 轴相交于点
轴相交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,横、纵坐标均为整数的点叫做格点,若函数![]() 的图象恰好经过
的图象恰好经过![]() 个格点,则称函数
个格点,则称函数![]() 为
为![]() 阶格点函数.下列函数中为一阶格点函数的是( )
阶格点函数.下列函数中为一阶格点函数的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() .由直线
.由直线![]() 上离圆心最近的点
上离圆心最近的点![]() 向圆
向圆![]() 引切线,切点为
引切线,切点为![]() ,则线段
,则线段![]() 的长为__________.
的长为__________.
【答案】![]()
【解析】圆心![]() 到直线
到直线![]() 的距离:
的距离:![]() ,
,
结合几何关系可得线段![]() 的长度为
的长度为![]() .
.
【题型】填空题
【结束】
16
【题目】设![]() 是两个非零平面向量,则有:
是两个非零平面向量,则有:
①若![]() ,则
,则![]()
②若![]() ,则
,则![]()
③若![]() ,则存在实数
,则存在实数![]() ,使得
,使得![]()
④若存在实数![]() ,使得
,使得![]() ,则
,则![]() 或
或![]() 四个命题中真命题的序号为 __________.(填写所有真命题的序号)
四个命题中真命题的序号为 __________.(填写所有真命题的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com