
ΓΨΧβΡΩΓΩάœ Π‘ΎΥΡΗω≤ΜΆ§ΒΡΚ–Ή”άοΟφΖ≈ΝΥ4’≈≤ΜΆ§ΒΡΤΥΩΥ≈ΤΘ§Ζ÷±π «ΚλΧ“![]() Θ§ΟΖΜ®
Θ§ΟΖΜ®![]() Θ§ΖΫΤ§
Θ§ΖΫΤ§![]() “‘ΦΑΚΎΧ“
“‘ΦΑΚΎΧ“![]() Θ§»ΟΟςΓΔ–ΓΚλΓΔ–Γ’≈ΓΔ–ΓάνΥΡΗω»ΥΫχ––≤¬≤βΘΚ
Θ§»ΟΟςΓΔ–ΓΚλΓΔ–Γ’≈ΓΔ–ΓάνΥΡΗω»ΥΫχ––≤¬≤βΘΚ
–ΓΟςΥΒΘΚΒΎ1ΗωΚ–Ή”άοΟφΖ≈ΒΡ «ΟΖΜ®![]() Θ§ΒΎ3ΗωΚ–Ή”άοΟφΖ≈ΒΡ «ΖΫΤ§
Θ§ΒΎ3ΗωΚ–Ή”άοΟφΖ≈ΒΡ «ΖΫΤ§![]() ΘΜ
ΘΜ
–ΓΚλΥΒΘΚΒΎ2ΗωΚ–Ή”άοΟφΖΙΒΡ «ΟΖΜ®![]() Θ§ΒΎ3ΗωΚ–Ή”άοΖ≈ΒΡ «ΚΎΧ“
Θ§ΒΎ3ΗωΚ–Ή”άοΖ≈ΒΡ «ΚΎΧ“![]() ΘΜ
ΘΜ
–Γ’≈ΥΒΘΚΒΎ4ΗωΚ–Ή”άοΟφΖ≈ΒΡ «ΚΎΧ“![]() Θ§ΒΎ2ΗωΚ–Ή”άοΟφΖ≈ΒΡ «ΖΫΤ§
Θ§ΒΎ2ΗωΚ–Ή”άοΟφΖ≈ΒΡ «ΖΫΤ§![]() ΘΜ
ΘΜ
–ΓάνΥΒΘΚΒΎ4ΗωΚ–Ή”άοΟφΖ≈ΒΡ «ΚλΧ“![]() Θ§ΒΎ3ΗωΚ–Ή”άοΟφΖ≈ΒΡ «ΖΫΤ§
Θ§ΒΎ3ΗωΚ–Ή”άοΟφΖ≈ΒΡ «ΖΫΤ§![]() ΘΜ
ΘΜ
άœ ΠΥΒΘΚΓΑ–ΓΟςΓΔ–ΓΚλΓΔ–Γ’≈ΓΔ–ΓάνΘ§ΡψΟ«ΕΦ÷ΜΥΒΕ‘ΝΥ“ΜΑκΘ°Γ±‘ρΩ…“‘ΆΤ≤βΘ§ΒΎ4ΗωΚ–Ή”άοΉΑΒΡ «Θ® Θ©
A. ΚλΧ“![]() ΜρΚΎΧ“
ΜρΚΎΧ“![]() B. ΚλΧ“
B. ΚλΧ“![]() ΜρΟΖΜ®
ΜρΟΖΜ®![]()
C. ΚΎΧ“![]() ΜρΖΫΤ§
ΜρΖΫΤ§![]() D. ΚΎΧ“
D. ΚΎΧ“![]() ΜρΟΖΜ®
ΜρΟΖΜ®![]()
ΓΨ¥πΑΗΓΩA
ΓΨΫβΈωΓΩ“ρΈΣΥΡΗω»ΥΕΦ÷Μ≤¬Ε‘ΝΥ“ΜΑκΘ§Ι ”–“Μœ¬ΝΫ÷÷Ω…ΡήΘΚ
Θ®1Θ©Β±–ΓΟς≤¬Ε‘ΒΎ1ΗωΚ–Ή”άοΟφΖ≈ΒΡ «ΟΖΜ®A ±Θ§ΒΎ3ΗωΚ–Ή”άοΟφΖ≈ΒΡ≤Μ «ΖΫΤ§AΘ§‘ρ–Γάν≤¬Ε‘ΒΎ4ΗωΚ–Ή”άοΟφΖ≈ΒΡ ±ΚλΧ“AΘ§–Γ’≈≤¬Ε‘ΒΎ2ΗωΚ–Ή”άοΟφΖ≈ΒΡ «ΖΫΤ§AΘ§–ΓΚλ≤¬Ε‘ΒΎ3ΗωΚ–Ή”άοΟφΖ≈ΒΡ «ΚΎΧ“AΘΜ
Θ®2Θ©»τ–ΓΟς≤¬Ε‘ΒΡ «ΒΎ3ΗωΚ–Ή”άοΟφΖ≈ΒΡ «ΖΫΤ§AΘ§‘ρΒΎ1ΗωΚ–Ή”άοΟφΖ≈ΒΡ≤Μ «ΟΖΜ®A,–ΓΚλ≤¬Ε‘ΒΎ2ΗωΚ–Ή”άοΟφΖ≈ΒΡ «ΟΖΜ®AΘ§–Γ’≈≤¬Ε‘ΒΎ4ΗωΚ–Ή”άοΟφΖ≈ΒΡ «ΚΎΧ“AΘ§–Γάν≤¬Ε‘ΒΎ3ΗωΚ–Ή”άοΟφΖ≈ΒΡ «ΖΫΤ§A,‘ρΒΎ“ΜΗωΚ–Ή”÷ΜΡή «ΚλΧ“A,
Ι ―ΓA.


 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§Ρ≥Ιψ≥Γ÷–Φδ”–“ΜΩι±Ώ≥ΛΈΣ2ΑΌΟΉΒΡΝβ–ΈΉ¥¬ΧΜ·«χ![]() Θ§Τδ÷–
Θ§Τδ÷–![]() «ΑκΨΕΈΣ1ΑΌΟΉΒΡ…»–ΈΘ§
«ΑκΨΕΈΣ1ΑΌΟΉΒΡ…»–ΈΘ§![]() Θ° Ιήάμ≤ΩΟ≈”ϊ‘ΎΗΟΒΊ¥”
Θ° Ιήάμ≤ΩΟ≈”ϊ‘ΎΗΟΒΊ¥”![]() ΒΫ
ΒΫ![]() –όΫ®–Γ¬ΖΘΚ‘ΎΜΓ
–όΫ®–Γ¬ΖΘΚ‘ΎΜΓ![]() …œ―Γ“ΜΒψ
…œ―Γ“ΜΒψ![]() Θ®“λ”Ύ
Θ®“λ”Ύ![]() ΝΫΒψΘ©Θ§ΙΐΒψ
ΝΫΒψΘ©Θ§ΙΐΒψ![]() –όΫ®”κ
–όΫ®”κ![]() ΤΫ––ΒΡ–Γ¬Ζ
ΤΫ––ΒΡ–Γ¬Ζ![]() Θ°Έ ΘΚΒψ
Θ°Έ ΘΚΒψ![]() ―Γ‘ώ‘ΎΚΈ¥Π ±Θ§≤≈Ρή ΙΒΟ–όΫ®ΒΡ–Γ¬Ζ
―Γ‘ώ‘ΎΚΈ¥Π ±Θ§≤≈Ρή ΙΒΟ–όΫ®ΒΡ–Γ¬Ζ![]() ”κ
”κ![]() ΦΑ
ΦΑ![]() ΒΡΉή≥ΛΉν–ΓΘΩ≤ΔΥΒΟςάμ”…Θ°
ΒΡΉή≥ΛΉν–ΓΘΩ≤ΔΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐf(x)ΘΫx2ΘΪ(xΘ≠1)|xΘ≠a|.
(1)»τaΘΫΘ≠1Θ§ΫβΖΫ≥Χf(x)ΘΫ1ΘΜ
(2)»τΚ· ΐf(x)‘ΎR…œΒΞΒςΒί‘ωΘ§«σ Β ΐaΒΡ»Γ÷ΒΖΕΈßΘΜ
(3) «Ζώ¥φ‘Ύ Β ΐaΘ§ Ι≤ΜΒ» Ϋf(x)Γί2xΘ≠3Ε‘»Έ“βxΓ RΚψ≥…ΝΔΘΩ»τ¥φ‘ΎΘ§«σ≥ωaΒΡ»Γ÷ΒΖΕΈßΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() Θ®Τδ÷–
Θ®Τδ÷–![]() Θ§
Θ§ ![]() ΈΣ≥Θ ΐΘ§
ΈΣ≥Θ ΐΘ§ ![]() ΈΣΉ‘»ΜΕ‘ ΐΒΡΒΉ ΐΘ©.
ΈΣΉ‘»ΜΕ‘ ΐΒΡΒΉ ΐΘ©.
Θ®1Θ©Χ÷¬έΚ· ΐ![]() ΒΡΒΞΒς–‘ΘΜ
ΒΡΒΞΒς–‘ΘΜ
Θ®2Θ©…η«ζœΏ![]() ‘Ύ
‘Ύ![]() ¥ΠΒΡ«–œΏΈΣ
¥ΠΒΡ«–œΏΈΣ![]() Θ§Β±
Θ§Β±![]() ±Θ§«σ÷±œΏ
±Θ§«σ÷±œΏ![]() ‘Ύ
‘Ύ![]() ÷α…œΫΊΨύΒΡ»Γ÷ΒΖΕΈß.
÷α…œΫΊΨύΒΡ»Γ÷ΒΖΕΈß.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΦ·ΚœA «Κ· ΐy=lgΘ®20©¹8x©¹x2Θ©ΒΡΕ®“ε”ρΘ§Φ·ΚœB «≤ΜΒ» Ϋx2©¹2x+1©¹a2Γί0Θ®aΘΨ0Θ©ΒΡΫβΦ·Θ§pΘΚxΓ AΘ§qΘΚxΓ BΘ°
Θ®1Θ©»τAΓ…B=Θ§«σ Β ΐaΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®2Θ©»τ©Vp «qΒΡ≥δΖ÷≤Μ±Ί“ΣΧθΦΰΘ§«σ Β ΐaΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() ‘Ύ
‘Ύ![]() ¥Π»ΓΒΟΦΪ¥σ÷ΒΘ§‘ρ Β ΐ
¥Π»ΓΒΟΦΪ¥σ÷ΒΘ§‘ρ Β ΐ![]() ΒΡ»Γ÷ΒΖΕΈß «Θ® Θ©
ΒΡ»Γ÷ΒΖΕΈß «Θ® Θ©
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΘ®±Ψ–ΓΧβ¬ζΖ÷13Ζ÷Θ©
“―÷ΣΚ· ΐ![]() Θ§Τδ÷–
Θ§Τδ÷–![]() Θ°
Θ°
Θ®ΔώΘ©Β±![]() ±Θ§«σ«ζœΏ
±Θ§«σ«ζœΏ![]() ‘ΎΒψ
‘ΎΒψ![]() ¥ΠΒΡ«–œΏΖΫ≥ΧΘΜ
¥ΠΒΡ«–œΏΖΫ≥ΧΘΜ
Θ®ΔρΘ©÷ΛΟςΘΚ ![]() ‘Ύ«χΦδ
‘Ύ«χΦδ![]() …œ«Γ”–
…œ«Γ”–![]() ΗωΝψΒψΘ°
ΗωΝψΒψΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
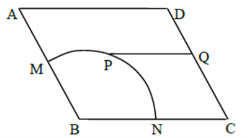
ΓΨΧβΡΩΓΩ»γΆΦΘ§’ΐΖΫΧεABCD-A1B1C1D1ΒΡάβ≥ΛΈΣ1Θ§œΏΕΈB1D1…œ”–ΝΫΗωΕ·ΒψEΘ§FΘ§«“EF=![]() Θ§‘ρœ¬Ν–Ϋα¬έ÷–¥μΈσΒΡ «(ΓΓΓΓ)
Θ§‘ρœ¬Ν–Ϋα¬έ÷–¥μΈσΒΡ «(ΓΓΓΓ)
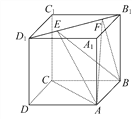
A. ACΓΆBE
B. EFΓΈΤΫΟφABCD
C. »ΐάβΉΕA-BEFΒΡΧεΜΐΈΣΕ®÷Β
D. ΓςAEFΒΡΟφΜΐ”κΓςBEFΒΡΟφΜΐœύΒ»
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘Ύ ΐΝ–{an}÷–Θ§a1ΘΫ1Θ§a2ΘΫ![]() Θ§anΘΪ1Θ≠
Θ§anΘΪ1Θ≠![]() anΘΪanΘ≠1ΘΫ0 (nΓί2Θ§«“nΓ N*)Θ§»τ ΐΝ–{anΘΪ1ΘΪΠΥan} «Β»±» ΐΝ–Θ°
anΘΪanΘ≠1ΘΫ0 (nΓί2Θ§«“nΓ N*)Θ§»τ ΐΝ–{anΘΪ1ΘΪΠΥan} «Β»±» ΐΝ–Θ°
(1)«σ Β ΐΠΥΘΜ
(2)«σ ΐΝ–{an}ΒΡΆ®œνΙΪ ΫΘΜ
(3)…η![]() Θ§«σ÷ΛΘΚ
Θ§«σ÷ΛΘΚ ![]() .
.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com