
【题目】已知四棱锥P﹣ABCD及其三视图如下图所示,E是侧棱PC上的动点.
(Ⅰ)求四棱锥P﹣ABCD的体积;
(Ⅱ)不论点E在何位置,是否都有BD⊥AE?试证明你的结论;
(Ⅲ)若点E为PC的中点,求二面角D﹣AE﹣B的大小.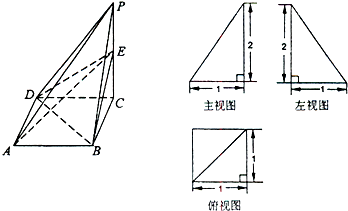
【答案】解:(I)由三视图知PC⊥面ABCD,
ABCD为正方形,且PC=2,AB=BC=1,
∴ ![]() .
.
(II)不论点E在何位置,都有BD⊥AE.
证明如下:
∵PC⊥面ABCD,BD面ABCD,∴PC⊥BD
而BD⊥AC,AC∩AE=A,∴BD⊥面ACE,
而AE面ACE,
∴BD⊥AE.
(III)连接AC,交BD于O.
由对称性,二面角D﹣AE﹣B是二面角O﹣AE﹣B的2倍,
设θ为二面角O﹣AE﹣B的平面角.
注意到B在面ACE上的射影为O,![]() ,
,![]() ,
,
∴ ![]() ,
,
∴θ=60°∴二面角D﹣AE﹣B是120°.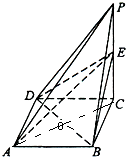
【解析】(I)由三视图知PC⊥面ABCD,ABCD为正方形,且PC=2,AB=BC=1,由此能求出四棱锥P﹣ABCD的体积.(II)不论点E在何位置,都有BD⊥AE.由已知得PC⊥BD,从而BD⊥面ACE,由此能证明BD⊥AE.(III)连接AC,交BD于O.由对称性,二面角D﹣AE﹣B是二面角O﹣AE﹣B的2倍,设θ为二面角O﹣AE﹣B的平面角.注意到B在面ACE上的射影为O,由 ![]() ,能求出二面角D﹣AE﹣B的大小.
,能求出二面角D﹣AE﹣B的大小.


科目:高中数学 来源: 题型:
【题目】某产品共有100件,其中一、二、三、四等品的个数比为4:3:2:1,采用分层抽样的方法抽取一个样本,若从一等品中抽取8件,从三等品和四等品中抽取的个数分别为a,b,则直线ax+by+8=0上的点到原点的最短距离为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,已知a1=1, ![]() ,
,
(1)求证数列{ ![]() }是等差数列;
}是等差数列;
(2)求数列{an}的通项公式;
(3)若对一切n∈N* , 等式a1b1+a2b2+a3b3+…+anbn=2n恒成立,求数列{bn}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】暑假期间小辉计划在8月11日至8月20日期间调研某商业中心周边停车场停车状况,根据停车场统计数据,该停车场在此期间“停车难易度”(即停车数量与核定的最大瞬时容量之比,40%以下为较易,40%~60%为一般,60%以上为较难),情况如图所示,小辉随机选择8月11日至8月19日中的某一天达到该商业中心,并连续调研2天.
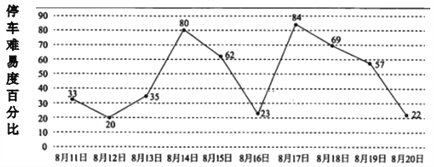
(Ⅰ)求小辉连续两天都遇上停车场较难的概率;
(Ⅱ)设![]() 是小辉调研期间遇上停车较易的天数,求
是小辉调研期间遇上停车较易的天数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)由图判断从哪天开始连续三天停车难易度的方差最大?(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)=Asin(ωx+φ)(x>0,A>0)的图象如图所示. 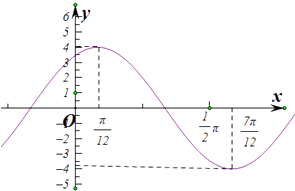
(1)求函数f(x)的解析式;
(2)写出函数f(x)的单调递增区间
(3)设不相等的实数,x1 , x2∈(0,π),且f(x1)=f(x2)=﹣2,求x1+x2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象在点
的图象在点![]() 处的切线方程为
处的切线方程为![]() .
.
(Ⅰ)求实数![]() 、
、![]() 的值;
的值;
(Ⅱ)求函数![]() 在区间
在区间![]() 上的最大值;
上的最大值;
(Ⅲ)曲线![]() 上存在两点
上存在两点![]() 、
、![]() ,使得
,使得![]() 是以坐标原点
是以坐标原点![]() 为直角顶点的直角三角形,且斜边
为直角顶点的直角三角形,且斜边![]() 的中点在
的中点在![]() 轴上,求实数
轴上,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,左右焦点分别为
,左右焦点分别为![]() 是椭圆在第一象限上的一个动点,圆
是椭圆在第一象限上的一个动点,圆![]() 与
与![]() 的延长线,
的延长线, ![]() 的延长线以及线段
的延长线以及线段![]() 都相切,
都相切, ![]() 为一个切点.
为一个切点.
(1)求椭圆方程;
(2)设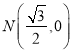 ,过
,过![]() 且不垂直于坐标轴的动点直线
且不垂直于坐标轴的动点直线![]() 交椭圆于
交椭圆于![]() 两点,若以
两点,若以![]() 为邻边的平行四边形是菱形,求直线
为邻边的平行四边形是菱形,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com