对于任意实数a,关于x的方程log2[2x2+(m+3)x+2m]=a总有实数解,则实数m的取值范围是________.
{m|m≤1或m≥9}
分析:由对于任意实数a,关于x的方程log
2[2x
2+(m+3)x+2m]=a总有实数解,知y=log
2[2x
2+(m+3)x+2m]的值域为R.所以∴2x
2+(m+3)x+2m必须至少取满(0,+∞).也就是说2x
2+(m+3)x+2m的最小值要小于等于0.由此能求出实数m的取值范围.
解答:∵对于任意实数a,关于x的方程log
2[2x
2+(m+3)x+2m]=a总有实数解,
∴y=log
2[2x
2+(m+3)x+2m]的值域为R.
∴2x
2+(m+3)x+2m必须至少取满(0,+∞).
也就是说2x
2+(m+3)x+2m的最小值要小于等于0.
对称轴 x=
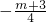
,
最小值
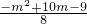
≤0,
即m
2-10m+9≥0,
解得m≤1或m≥9.
∴数m的取值范围是{m|m≤1或m≥9}.
故答案为:{m|m≤1或m≥9}.
点评:本题考查函数的恒成立问题,解题时要认真审题,仔细解答,注意对数函数的性质的灵活运用.

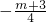 ,
,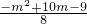 ≤0,
≤0,

 53随堂测系列答案
53随堂测系列答案