
(08年昆明市适应考试)(12分)设点![]() ,动圆
,动圆![]() 经过点
经过点![]() 且和直线
且和直线![]() :
:![]() 相切. 记动圆的圆心
相切. 记动圆的圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)设点![]() 为直线
为直线![]() 上的动点,过点
上的动点,过点![]() 作曲线
作曲线![]() 的切线
的切线![]() (
(![]() 为切点),
为切点),
证明:直线![]() 必过定点并指出定点坐标.
必过定点并指出定点坐标.
解析:(Ⅰ)过点![]() 作
作![]() 垂直直线
垂直直线![]() 于点
于点![]()
依题意得:![]() ,
,
所以动点![]() 的轨迹为是以
的轨迹为是以![]() 为焦点,直线
为焦点,直线![]() 为准线的抛物线,
为准线的抛物线,
即曲线![]() 的方程是
的方程是![]() ………………………4分
………………………4分
(Ⅱ)设![]() 、
、![]() ,
,![]() ,则
,则
由![]() 知,
知,![]() , ∴
, ∴![]() ,
,![]()
又∵切线AQ的方程为:![]() ,注意到
,注意到![]()
切线AQ的方程可化为:![]() ;
;
由![]() 在切线AQ上, ∴
在切线AQ上, ∴![]()
于是![]() 在直线
在直线![]() 上
上
同理,由切线BQ的方程可得:![]()
于是![]() 在直线
在直线![]() 上
上
所以,直线AB的方程为:![]() ,
,
又把![]() 代入上式得:
代入上式得:![]()
∴直线AB的方程为:![]()
∴直线AB必过定点![]() . ………………………12分
. ………………………12分
(Ⅱ)解法二:设![]() ,切点的坐标为
,切点的坐标为![]() ,则
,则
由![]() 知,
知,![]() ,得切线方程:
,得切线方程:![]()
即为:![]() ,又∵
,又∵![]() 在切线上,
在切线上,
所以可得:![]() ,又把
,又把![]() 代入上式得:
代入上式得:
![]() ,解之得:
,解之得:![]()
∴![]() ,
,![]()
故直线AB的方程为:![]()
化简得:![]()
∴直线AB的方程为:![]()
∴直线AB必过定点![]() .
.


科目:高中数学 来源: 题型:
(08年昆明市适应考试文) (12分)等差数列![]() 中,
中,![]() 为数列
为数列![]() 的前
的前![]() 项和,且满足
项和,且满足![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)设![]()
![]() ,
,![]() ,是否存在最大的整数
,是否存在最大的整数![]() ,使得对任意
,使得对任意![]() ,均有
,均有![]() 成立?若存在,求出
成立?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
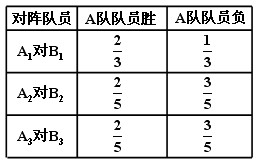
(08年昆明市适应考试文)(12分)在2008年北京奥运会某项目的选拔比赛中, ![]() 、
、![]() 两个代表队进行对抗赛. 每队三名队员.
两个代表队进行对抗赛. 每队三名队员. ![]() 队队员是
队队员是![]() ,
,![]() 队队员是
队队员是![]() . 按以往多次比赛的统计,对阵队员之间胜负概率如下表,现按表中对阵方式出场进行三场比赛,每场胜队得1分,负队得0分.
. 按以往多次比赛的统计,对阵队员之间胜负概率如下表,现按表中对阵方式出场进行三场比赛,每场胜队得1分,负队得0分.
(Ⅰ)求A 队得分为2分的概率;
(Ⅱ)分别求A 队得分不少于2分的概率及B队得分不多于2分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年昆明市适应考试)(12分)在数列![]() 中,已知
中,已知![]() ,
, ![]()
![]()
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)若![]() (
(![]() 为非零常数),问是否存在整数
为非零常数),问是否存在整数![]() ,使得对任意
,使得对任意![]() 都有
都有![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com