
如图,EP交圆于E、C两点,PD切圆于D,G为CE上一点且 ,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.
,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.
(1)求证:AB为圆的直径;
(2)若AC=BD,求证: .
.
(1)证明见解析;(2)证明见解析.
解析试题分析:
解题思路:(1)利用直径所对的圆周角为直角,证明 即可;(2)利用全等三角形即(1)结论证明
即可;(2)利用全等三角形即(1)结论证明 .
.
规律总结:本题考查几何证明中的直线与圆的位置关系,培养学生的观察能力以及分析问题的能力.
试题解析:(1)因为PD=PG,所以∠PDG=∠PGD.
由于PD为切线,故∠PDA=∠DBA,又由于∠PGD=∠EGA,故∠DBA=∠EGA,所以∠DBA+∠BAD=∠EGA+∠BAD,从而∠BDA=∠PFA.
由于AF垂直EP,所以∠PFA=90°,于是∠BDA=90°,故AB是直径.
(2)连接BC,DC.
由于AB是直径,故∠BDA=∠ACB=90°,
在Rt△BDA与Rt△ACB中,AB=BA,AC=BD,
从而Rt△BDA≌Rt△ACB,于是∠DAB=∠CBA.
又因为∠DCB=∠DAB,所以∠DCB=∠CBA,故DC∥AB.
由于
于是ED是直径,由(1)得ED=AB.
考点:直线与圆的位置关系.


科目:高中数学 来源: 题型:解答题
如图,已知C点在圆O直径BE的延长线上,CA切圆O于A点,DC是∠ACB的平分线交AE于点F,交AB于D点.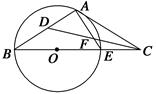
(1)求∠ADF的度数;
(2)AB=AC,求AC∶BC.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,EP交圆于E、C两点,PD切圆于D,G为CE上一点且 ,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.
,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.
(1)求证:AB为圆的直径;
(2)若AC=BD,求证:AB=ED.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,已知A、B、C三点的坐标分别为(0,1)、(-1,0)、(1,0),P是线段AC上一点,BP交AO于点D,设三角形ADP的面积为S,点P的坐标为(x,y),求S关于x的函数表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com