
(本题满分10分)
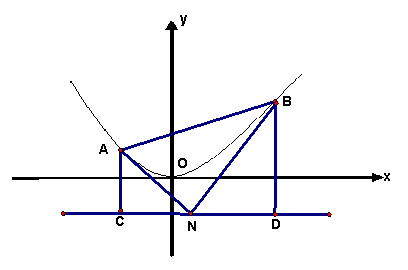
如图,已知抛物线M:![]() 的准线为
的准线为![]() ,N为
,N为![]() 上的一个动点,过点N作抛物线M的两条切线,切点分别为A、B,再分别过A、B两点作
上的一个动点,过点N作抛物线M的两条切线,切点分别为A、B,再分别过A、B两点作![]() 的垂线,垂足分别为C,D。
的垂线,垂足分别为C,D。
求证:直线AB必经过y轴上的一个定点Q,并写出点Q的坐标;
若![]() 的面积成等差数列,求此时点N的坐标。
的面积成等差数列,求此时点N的坐标。
【必做题】
解法一:(1)因为抛物线的准线![]() 的方程为
的方程为![]() ,
,
所以可设点![]() 的坐标分别为
的坐标分别为![]() ,
,
![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
由![]() ,得
,得![]() ,求导数得
,求导数得![]() ,于是
,于是![]() ,
,
 即
即 ,化简得
,化简得![]() ,
,
同理可得![]() ,
,
所以![]() 和
和![]() 是关于
是关于![]() 的方程
的方程![]()
两个实数根,所以![]() ,
,
且![]() .
.
在直线![]() 的方程
的方程![]() 中,
中,
令![]() ,得
,得![]() =
=![]() 为定值,
为定值,
所以直线![]() 必经过
必经过![]() 轴上的一个定点
轴上的一个定点![]() ,即抛物线的焦点.……………………………5分
,即抛物线的焦点.……………………………5分
(2)由(1)知![]() ,所以
,所以![]() 为线段
为线段![]() 的中点,取线段
的中点,取线段![]() 的中点
的中点![]() ,
,
因为![]() 是抛物线的焦点,所以
是抛物线的焦点,所以![]() ,所以
,所以![]() ,
,
所以![]()
![]()
![]() ,
,
又因为![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() 成等差数列,即
成等差数列,即![]() 成等差数列,
成等差数列,
即![]() 成等差数列,所以
成等差数列,所以![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
![]() 时,
时,![]() ,
,![]() ,
,
![]() 时,
时,![]() ,
,![]() ,
,
所以所求点![]() 的坐标为
的坐标为![]() .………………………………………………………………10分
.………………………………………………………………10分
解法二:(1)因为已知抛物线的准线![]() 的方程为
的方程为![]() ,所以可设点
,所以可设点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
设过![]() 点与抛物线相切的直线方程为
点与抛物线相切的直线方程为![]() ,与抛物线方程
,与抛物线方程![]() 联立,消去
联立,消去![]() 得
得![]() ,
,
因为直线与抛物线相切,所以![]() ,即
,即![]() ,解得
,解得 ,此时两切点横坐标分别为
,此时两切点横坐标分别为![]() ,
,
在直线![]() 的方程
的方程![]() 中,令
中,令![]() 得
得
![]() =
=![]() 为定值,
为定值,
所以直线![]() 必经过
必经过![]() 轴上的一个定点
轴上的一个定点![]() ,即抛物线的焦点.……………………………5分
,即抛物线的焦点.……………………………5分
(2)由(1)知两切线的斜率分别为 ,则
,则![]() ,所以
,所以![]() ,
,
连接![]() ,则直线
,则直线![]() 斜率为
斜率为![]() ,
,
又因为直线![]() 的斜率
的斜率![]() ,
,
所以![]() ,
,
所以![]() ,又因为
,又因为![]() ,所以
,所以![]() ,
,
所以![]() 和
和![]() 的面积成等差数列,所以
的面积成等差数列,所以![]() 成等差数列,
成等差数列,
所以![]() 成等差数列,所以
成等差数列,所以![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
![]() 时,
时,![]() ,
,![]() ,
,
![]() 时,
时,![]() ,
,![]() ,
,
所以所求点![]() 的坐标为
的坐标为![]() . …………………………………………………………10分
. …………………………………………………………10分
(以上各题如考生另有解法,请参照本评分标准给分)


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
17.本题满分10分已知函数![]() 的图象在y轴上的截距为
的图象在y轴上的截距为![]() ,相邻的两个最值点是
,相邻的两个最值点是![]() 和
和![]() (1)求函数
(1)求函数![]() ;(2)设
;(2)设![]() ,问将函数
,问将函数![]() 的图像经过怎样的变换可以得到
的图像经过怎样的变换可以得到![]() 的图像?(3)画出函数
的图像?(3)画出函数![]() 在区间
在区间![]() 上的简图.
上的简图.
查看答案和解析>>
科目:高中数学 来源:2014届浙江省高二下学期期中考试理科数学试卷(解析版) 题型:解答题
(本题满分10分)
(Ⅰ)设 ,求证:
,求证: ;
;
(Ⅱ)设 ,求证:三数
,求证:三数 ,
, ,
, 中至少有一个不小于2.
中至少有一个不小于2.
查看答案和解析>>
科目:高中数学 来源:2014届河南省高二上学期期末考试理科数学试卷(解析版) 题型:解答题
(本题满分10分)
如图,已知正四棱柱ABCD—A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F,

⑴求证:A1C⊥平面BDE;
⑵求A1B与平面BDE所成角的正弦值。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省扬州市宝应县高三下学期期初测试数学试卷 题型:解答题
(本题满分10分)
如图,已知正三棱柱 的所有棱长都为2,
的所有棱长都为2, 为棱
为棱 的中点,
的中点,
(1)求证: 平面
平面 ;
;
(2)求二面角 的余弦值大小.
的余弦值大小.

查看答案和解析>>
科目:高中数学 来源:2010-2011年辽宁省高二上学期期末考试数学理卷 题型:解答题
(本题满分10分)
如图,要计算西湖岸边两景点 与
与 的距离,由于地形的限制,需要在岸上选取
的距离,由于地形的限制,需要在岸上选取 和
和 两点,现测得
两点,现测得 ,
, ,
, ,
, ,
, ,求两景点
,求两景点 与
与 的距离(精确到0.1km).参考数据:
的距离(精确到0.1km).参考数据:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com