
分析 (1)根据题意,分析可得$\sqrt{(x-\sqrt{2})^{2}+{y}^{2}}$+$\sqrt{(x+\sqrt{2})^{2}+{y}^{2}}$=2$\sqrt{3}$,由椭圆的定义可得点P(x,y)对应的曲线方程C是椭圆,进而由题意可得a、c的值,计算可得b的值,代入椭圆的标准方程即可得答案;
(2)根据题意,分2种情况讨论:、①当直线l的斜率不存在时,直线l的方程为x=1,代入椭圆的方程可得A,B两点的坐标,计算可得k1+k2的值,②当直线l的斜率存在时,设直线l的方程为y=k(x-1),联立直线与椭圆的方程,可得(3k2+1)x2-6k2x+3k2-3=0.由根与系数的关系分析可得x1+x2=$\frac{6{k}^{2}}{3{k}^{2}+1}$,x1x2=$\frac{3{k}^{2}-3}{3{k}^{2}+1}$.结合直线的方程可得k1+k2═$\frac{2-{y}_{1}}{3-{x}_{1}}$+$\frac{2-{y}_{2}}{3-{x}_{2}}$,将其变形化简可得k1+k2的值,综合2种情况即可得答案.
解答 解:(1)、依题意:三个数$\sqrt{(x-\sqrt{2})^{2}+{y}^{2}}$,$\sqrt{3}$,$\sqrt{(x+\sqrt{2})^{2}+{y}^{2}}$成等差数列,
则有$\sqrt{(x-\sqrt{2})^{2}+{y}^{2}}$+$\sqrt{(x+\sqrt{2})^{2}+{y}^{2}}$=2$\sqrt{3}$,
所以点P(x,y)对应的曲线方程C是椭圆,
得$\left\{\begin{array}{l}{a=\sqrt{3}}\\{c=\sqrt{2}}\end{array}\right.$.
故b=1
椭圆C方程为$\frac{{x}^{2}}{3}$+y2=1,
(2)、①当直线l的斜率不存在时,直线l的方程为x=1.由$\left\{\begin{array}{l}{x=1}\\{\frac{{x}^{2}}{3}+{y}^{2}=1}\end{array}\right.$解得$\left\{\begin{array}{l}x=1\\ y=±\frac{\sqrt{6}}{3}.\end{array}$
不妨设A(1,$\frac{\sqrt{6}}{3}$),B(1,-$\frac{\sqrt{6}}{3}$),
因为k1+k2=2,
②当直线l的斜率存在时,设直线l的方程为y=k(x-1).
将y=k(x-1)代入$\frac{{x}^{2}}{3}$+y2=1,
整理得(3k2+1)x2-6k2x+3k2-3=0.
设A(x1,y1),B(x2,y2),则x1+x2=$\frac{6{k}^{2}}{3{k}^{2}+1}$,x1x2=$\frac{3{k}^{2}-3}{3{k}^{2}+1}$.
又y1=k(x1-1),y2=k(x2-1),
所以k1+k2=$\frac{2-{y}_{1}}{3-{x}_{1}}$+$\frac{2-{y}_{2}}{3-{x}_{2}}$
=$\frac{(2-{y}_{1})(3-{x}_{2})+(2-{y}_{2})(3-{x}_{1})}{(3-{x}_{1})(3-{x}_{2})}$
=$\frac{[2-k({x}_{1}-1)](3-{x}_{2})+[2-k({x}_{2}-1)](3-{x}_{1})}{{x}_{1}{x}_{2}-3({x}_{1}+{x}_{2})+9}$
=$\frac{2(12{k}^{2}+6)}{12{k}^{2}+6}$=2
即k1+k2=2,
综合可得:其k1+k2值为定植为2.
点评 本题考查椭圆与直线的位置关系,涉及椭圆的定义以及标准方程,(2)中不能忽略直线斜率不存在的情况.


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:选择题
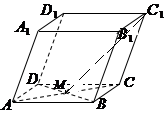 四棱柱ABCD-A1B1C1D1的底面是平行四边形,M是AC与BD的交点.若$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow b$,$\overrightarrow{A{A_1}}$=$\overrightarrow c$,则$\overrightarrow{{C_1}M}$可以表示为( )
四棱柱ABCD-A1B1C1D1的底面是平行四边形,M是AC与BD的交点.若$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow b$,$\overrightarrow{A{A_1}}$=$\overrightarrow c$,则$\overrightarrow{{C_1}M}$可以表示为( )| A. | $\overrightarrow a+\overrightarrow b+\frac{1}{2}\overrightarrow c$ | B. | $-\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b+\overrightarrow c$ | C. | $-\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b-\overrightarrow c$ | D. | $\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\overrightarrow c$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1,8,10} | B. | {1,2,4,6} | C. | {0,8,10} | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com