
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,若 ![]() (acosB+bcosA)=2csinC,a+b=4,且△ABC的面积的最大值为
(acosB+bcosA)=2csinC,a+b=4,且△ABC的面积的最大值为 ![]() ,则此时△ABC的形状为( )
,则此时△ABC的形状为( )
A.锐角三角形
B.直线三角形
C.等腰三角形
D.正三角形
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:高中数学 来源: 题型:
【题目】设定义在R上的函数f(x)是最小正周期2π的偶函数,f′(x)是函数f(x)的导函数,当x∈[0,π]时,0<f(x)<1;当x∈(0,π),且x≠ ![]() 时,(x﹣
时,(x﹣ ![]() )f′(x)>0,则函数y=f(x)﹣sinx在[﹣2π,2π]上的零点个数为( )
)f′(x)>0,则函数y=f(x)﹣sinx在[﹣2π,2π]上的零点个数为( )
A.2
B.4
C.5
D.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=4x,过焦点F作与x轴垂直的直线l1 , C上任意一点P(x0 , y0)(y0≠0)处的切线为l,l与l1交于M,l与准线交于N,则 ![]() = .
= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() .
.
(1)求f(f( ![]() ));
));
(2)若x0满足f(f(x0))=x0 , 且f(x0)≠x0 , 则称x0为f(x)的二阶不动点,求函数f(x)的二阶不动点的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图:四棱锥P﹣ABCD中,底面ABCD是平行四边形,且AC=BD,PA⊥底面ABCD,PA=AB=1, ![]() ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动. 
(1)证明:当点E在边BC上移动时,总有EF⊥AF;
(2)当CE等于何值时,PA与平面PDE所成角的大小为45°.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】春节是旅游消费旺季,某大型商场通过对春节前后20天的调查,得到部分日经济收入Q与这20天中的第x天(x∈N+)的部分数据如表:
天数x(天) | 3 | 5 | 7 | 9 | 11 | 13 | 15 |
日经济收入Q(万元) | 154 | 180 | 198 | 208 | 210 | 204 | 190 |
(1)根据表中数据,结合函数图象的性质,从下列函数模型中选取一个最恰当的函数模型描述Q与x的变化关系,只需说明理由,不用证明. ①Q=ax+b,②Q=﹣x2+ax+b,③Q=ax+b,④Q=b+logax.
(2)结合表中的数据,根据你选择的函数模型,求出该函数的解析式,并确定日经济收入最高的是第几天;并求出这个最高值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos2A﹣3cos(B+C)=1. (Ⅰ)求角A的大小;
(Ⅱ)若△ABC的面积S=5 ![]() ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,AB∥CD,∠ADC=90°,PD=AD=AB=1,DC=2. 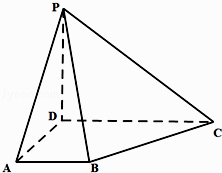
(1)求证:BC⊥平面PBD;
(2)求二面角A﹣PB﹣C的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com