解答时应写出必要的文字说明、证明过程或演算步骤
设函数f(x)＝ax3＋bx2＋cx＋d(a、b、c、d∈R)满足：
都有f(x)＋f(－x)＝0，且x＝1时，f(x)取极小值
(1)f(x)的解析式；
(2)当x∈[－1，1]时，证明：函数图象上任意两点处的切线不可能互相垂直；
(3)设F(x)＝|xf(x)|，证明：
时，
科目：高中数学 来源：2008届第一次六校联考高三数学文科试卷(广州深圳中山珠海惠州) 题型：044
解答时应写出必要的文字说明、证明过程或演算步骤
如图平面ABCD⊥平面ABEF，ABCD是正方形，ABEF是矩形，且AF＝
AD＝2，G是EF的中点，
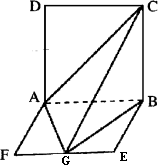
(1)求证平面AGC⊥平面BGC；
(2)求空间四边形AGBC的体积．
查看答案和解析>>
科目：高中数学 来源：2008届第一次六校联考高三数学文科试卷(广州深圳中山珠海惠州) 题型：044
解答时应写出必要的文字说明、证明过程或演算步骤
已知向量
＝(cos
x，sinx)，
＝(
)，且x∈[0，
]．
(1)求
(2)设函数
＋
，求函数f(x)的最值及相应的x的值．
查看答案和解析>>
科目：高中数学 来源：2008届第一次六校联考高三数学文科试卷(广州深圳中山珠海惠州) 题型：044
解答时应写出必要的文字说明、证明过程或演算步骤
已知数列{an}是等比数列，a4＝e，如果a2，a7是关于x的方程：
两个实根，(e是自然对数的底数)
(1)求{an}的通项公式；
(2)设：bn＝lnan，Sn是数列{bn}的前n项的和，当：Sn＝n时，求n的值；
(3)对于(2)中的{bn}，设：cn＝bnbn+1bn+2，而Tn是数列{cn}的前n项和，求Tn的最大值，及相应的n的值．
查看答案和解析>>
科目：高中数学 来源：2008届第一次六校联考高三数学文科试卷(广州深圳中山珠海惠州) 题型：044
解答时应写出必要的文字说明、证明过程或演算步骤
已知圆M的方程为：(x＋3)2＋y2＝100及定点N(3，0)，动点P在圆M上运动，线段PN的垂直平分线交圆M的半径MP于Q点，设点Q的轨迹为曲线C．
(1)求曲线C的方程；
(2)试问：过点T(
)是否存在直线l，使直线l与曲线C交于A，B两点，且
，(O为坐标原点)若存在求出直线l的方程，不存在说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
成立，所以：
，
，得 
，
，得
从而，函数解析式为：
4分
，设：任意两数
是函数
图像上两点的横坐标，则这两点的切线的斜率分别是：
，所以，
，得：
知：
是函数
图像上任意两点的切线不可能垂直 9分
时，
且
此时
即
，取等号，故：
14分
