
| A. | mf(xn)>nf(xm) | B. | mf(xn)<nf(xm) | ||
| C. | mf(xn)=nf(xm) | D. | mf(xn)与nf(xm)大小不确定 |
分析 构造函数g(x),根据已知条件求出g(x)的单调性,从而判断出g(xm)>g(xn),得出结论即可.
解答 解:∵x>1时,xxf′(x)>ef(x)恒成立,
∴lnxf′(x)-$\frac{1}{x}$f(x)>0,(x>1),
令g(x)=$\frac{f(x)}{lnx}$,(x>1),
则g′(x)=$\frac{f′(x)lnx-\frac{1}{x}f(x)}{{(lnx)}^{2}}$>0,
g(x)在(1,+∞)递增,
由m>n>0,x>1得:xm>xn>1,
∴g(xm)>g(xn),
∴mf(xn)<nf(xm),
故选:B.
点评 本题考查了函数的单调性问题,考查导数的应用,构造函数g(x)是解题的关键,本题是一道中档题.


科目:高中数学 来源: 题型:解答题
| 商店名称 | A | B | C | D |
| 销售额(x)/千万元 | 2 | 3 | 5 | 6 |
| 利润额(y)/百万元 | 2 | 3 | 3 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 时间 | 二月上旬 | 二月中旬 | 二月下旬 | 三月上旬 |
| 旬平均气温x(℃) | 3 | 8 | 12 | 17 |
| 旬销售量y(件) | 55 | m | 33 | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
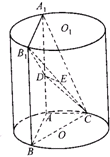 如图,AA1,BB1为圆柱OO1的母线,BC是底面圆O的直径,D、E分别是AA1、CB1的中点,且AB=AC=$\frac{1}{2}$AA1=2.
如图,AA1,BB1为圆柱OO1的母线,BC是底面圆O的直径,D、E分别是AA1、CB1的中点,且AB=AC=$\frac{1}{2}$AA1=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{a}{b}$>1 | B. | a2>b2 | C. | (${\frac{1}{2}}$)a<(${\frac{1}{2}}$)b | D. | lg(a-b)>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com