
| 日 期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
| 昼夜温差x(°C) | 10 | 11 | 13 | 12 | 8 | 6 |
| 就诊人数y(个) | 22 | 25 | 29 | 26 | 16 | 12 |
分析 (1)本题是一个古典概型,试验发生包含的事件是从6组数据中选取2组数据共有C62种情况,满足条件的事件是抽到相邻两个月的数据的情况有5种,根据古典概型的概率公式得到结果.
(2)根据所给的数据,求出x,y的平均数,根据求线性回归方程系数的方法,求出系数b,把b和x,y的平均数,代入求a的公式,做出a的值,写出线性回归方程.
解答 解:(1)由题意知本题是一个古典概型,
设抽到相邻两个月的数据为事件A
试验发生包含的事件是从6组数据中选取2组数据共有C62=15种情况,
每种情况都是等可能出现的其中,
满足条件的事件是抽到相邻两个月的数据的情况有5种
∴P(A)=${P_{(A)}}=\frac{5}{15}=\frac{1}{3}$
(2)由数据求得$\overline x=11,\overline y=24$,
由公式求得$\hat{b}$=$\frac{18}{7}$,
再由$\hat{a}$=$\overline{y}$-$\hat{b}$$\overline{x}$ 求得a=-$\frac{30}{7}$
∴y关于x的线性回归方程为$\widehaty=\frac{18}{7}x-\frac{30}{7}$
点评 本题考查线性回归方程的求法,考查等可能事件的概率,考查线性分析的应用,考查解决实际问题的能力,是一个综合题目,这种题目可以作为解答题出现在高考卷中


科目:高中数学 来源: 题型:解答题
| 金额分组 | [1,5) | [5,9) | [9,13) | [13,17) | [17,21) | [21,25] |
| 频数 | 3 | 9 | 17 | 11 | 8 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
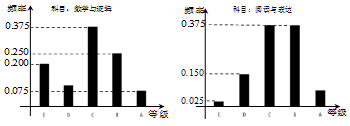
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4π | B. | 6π | C. | 8π | D. | 12π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | 3 | D. | $\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com