
分析 由题意画出图形,设M2(x,y),得到AB的方程,再由点M在线段AB上可得 x2+y2=4,在圆x2+y2=4上标出A,B所对应的点A′,B′,求出∠A′OB′,由弧长公式得答案.
解答 解:设点M2从A′开始运动,直到点B′结束,由题意知AB的方程为:x+y=4.设M2(x,y),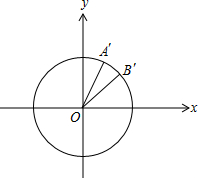
则M(x2,y2),由点M在线段AB上可得 x2+y2=4.
按照映射f:P(m,n)→${P}^{2}(\sqrt{m},\sqrt{n})$,可得 A(1,3)→A′(1,$\sqrt{3}$),B(2,2)→B′($\sqrt{2},\sqrt{2}$),
故tan∠A′OX=$\sqrt{3}$,∴∠A′OX=$\frac{π}{3}$.
tan∠B′OX=1,∴∠B′OX=$\frac{π}{4}$,故∠A′OB′=∠A′OX-∠B′OX=$\frac{π}{3}-\frac{π}{4}=\frac{π}{12}$,
∴点M的对应点M2所经过的路线长度为弧长$\widehat{A′B′}$=2×$\frac{π}{12}$=$\frac{π}{6}$,
故答案为:$\frac{π}{6}$.
点评 本题考查映射概念,解答此题的关键是对题意的正确理解,难度较大.


科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -8 | C. | 2 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sin4-cos4 | B. | cos4-sin4 | C. | ±sin4-cos4 | D. | sin4+cos4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x+3)2+(y-4)2=2 | B. | (x-3)2+(y+4)2=2 | C. | ${(x+3)^2}+{(y-4)^2}=\frac{1}{2}$ | D. | ${(x-3)^2}+{(y+4)^2}=\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 存在x>0,log3x>log4 | B. | 存在x>0,log3x≤log4 | ||
| C. | 任意x>0,log3x≤log4 | D. | 任意x>0,log3x=log4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com