
【题目】在四边形ABCD中,对角线AC,BD垂直相交于点O,且OA=OB=OD=4,OC=3. 将△BCD沿BD折到△BED的位置,使得二面角E﹣BD﹣A的大小为90°(如图).已知Q为EO的中点,点P在线段AB上,且 ![]() .
.
(Ⅰ)证明:直线PQ∥平面ADE;
(Ⅱ)求直线BD与平面ADE所成角θ的正弦值.
【答案】证明:(Ⅰ)如图,取OD的中点R,连接PR,QR,则DE∥RQ, 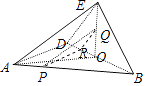
由题知 ![]() ,又
,又 ![]() ,故AB:AP=4:1=DB:DR,因此AD∥PR,
,故AB:AP=4:1=DB:DR,因此AD∥PR,
因为PR,RQ平面ADE,
且AD,DE平面ADE,故PR∥平面ADE,RQ∥平面ADE,
又PR∩RQ=R,
故平面PQR∥平面ADE,从而PQ∥平面ADE.
(Ⅱ)解:由题EA=ED=5, ![]() ,设点O到平面ADE的距离为d,
,设点O到平面ADE的距离为d,
则由等体积法可得 ![]() ,
,
故 ![]() ,因此
,因此 ![]() .
.
【解析】(Ⅰ)证明PR∥平面ADE,RQ∥平面ADE,可得平面PQR∥平面ADE,即可证明:直线PQ∥平面ADE;(Ⅱ)由等体积法可得点O到平面ADE的距离,即可求直线BD与平面ADE所成角θ的正弦值.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行,以及对空间角的异面直线所成的角的理解,了解已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则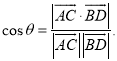 .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】为了巩固全国文明城市创建成果,今年吉安市开展了拆除违章搭建铁皮棚专项整治行为.为了了解市民对此项工作的“支持”与“反对”态度,随机从存在违章搭建的户主中抽取了男性、女性共![]() 名进行调查,调查结果如下:
名进行调查,调查结果如下:
支持 | 反对 | 合计 | |
男性 |
|
|
|
女性 |
|
|
|
合计 |
|
|
|
(1)根据以上数据,判断是否有![]() 的把握认为对此项工作的“支持”与“反对”态度与“性别”有关;
的把握认为对此项工作的“支持”与“反对”态度与“性别”有关;
(2)现从参与调查的女户主中按此项工作的“支持”与“反对”态度用分层抽样的方法抽取![]() 人,从抽取的
人,从抽取的![]() 人中再随机地抽取
人中再随机地抽取![]() 人赠送小礼品,记这
人赠送小礼品,记这![]() 人中持“支持”态度的有
人中持“支持”态度的有![]() 人,求
人,求![]() 的分布列与数学期望.
的分布列与数学期望.
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AD=AP,E为棱PD中点.
(1)求证:PD⊥平面ABE;
(2)若F为AB中点, ![]() ,试确定λ的值,使二面角P﹣FM﹣B的余弦值为-
,试确定λ的值,使二面角P﹣FM﹣B的余弦值为- ![]() .
. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的前n项和为
的前n项和为![]() ,
, ![]() ,
, ![]() ,数列
,数列![]() 满足:
满足: ![]() ,
, ![]() ,
, ![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]()
(1)求数列![]() 的通项公式及前n项和;
的通项公式及前n项和;
(2)求数列![]() 的通项公式及前n项和;
的通项公式及前n项和;
(3)记集合 ,若M的子集个数为16,求实数
,若M的子集个数为16,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学著作《九章算术》中有这样一个题目:“今有蒲生一日,长三尺;莞生一日,长一尺.蒲生日自半,莞生日自倍.问几何日而长等?”.其大意是“今有蒲生长1日,长为3尺;莞生长1日,长为1尺.蒲的生长逐日减其一半,莞的生长逐日增加一倍.问几日蒲、莞长度相等?”若本题改为求当蒲、莞长度相等时,莞的长度为( )
A. 4尺B. 5尺C. 6尺D. 7尺
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四边形ABCD中,对角线AC,BD垂直相交于点O,且OA=OB=OD=4,OC=3. 将△BCD沿BD折到△BED的位置,使得二面角E﹣BD﹣A的大小为90°(如图).已知Q为EO的中点,点P在线段AB上,且 ![]() .
.
(Ⅰ)证明:直线PQ∥平面ADE;
(Ⅱ)求直线BD与平面ADE所成角θ的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高一某班级在学校数学嘉年华活动中推出了一款数学游戏,受到大家的一致追捧.游戏规则如下:游戏参与者连续抛掷一颗质地均匀的骰子,记第i次得到的点数为![]() ,若存在正整数n,使得
,若存在正整数n,使得![]() ,则称为游戏参与者的幸运数字。
,则称为游戏参与者的幸运数字。
(I)求游戏参与者的幸运数字为1的概率;
(Ⅱ)求游戏参与者的幸运数字为2的概率,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com