
【题目】在“数学发展史”知识测验后,甲、乙、丙三人对成绩进行预测:
甲说:我的成绩比乙高;
乙说:丙的成绩比我和甲的都高;
丙说:我的成绩比乙高.
成绩公布后,三人成绩互不相同且只有一个人预测正确,那么三人中预测正确的是________.
【答案】甲.
【解析】
本题可从三人预测中互相关联的乙、丙两人的预测入手,因为只有一个人预测正确,而乙对则丙必对,丙对乙很有可能对,假设丙对乙错则会引起矛盾故只有一种情况就是甲预测正确乙、丙错误,即可求得答案.
由题意,可把三人的预测简写如下:
甲:甲![]() 乙.
乙.
乙:丙![]() 乙且丙
乙且丙![]() 甲.
甲.
丙:丙![]() 乙.
乙.
只有一个人预测正确,
![]() 分析三人的预测,可知:乙、丙的预测不正确.
分析三人的预测,可知:乙、丙的预测不正确.
如果乙预测正确,则丙预测正确,不符合题意.
如果丙预测正确,假设甲、乙预测不正确,
则有丙![]() 乙,乙
乙,乙![]() 甲,乙预测不正确,而丙
甲,乙预测不正确,而丙![]() 乙正确,
乙正确,
![]() 只有丙
只有丙![]() 甲不正确,
甲不正确,
![]() 甲
甲![]() 丙,这与丙
丙,这与丙![]() 乙,乙
乙,乙![]() 甲矛盾,不符合题意.
甲矛盾,不符合题意.
![]() 只有甲预测正确,乙、丙预测不正确,甲
只有甲预测正确,乙、丙预测不正确,甲![]() 乙,乙
乙,乙![]() 丙.
丙.
![]() 三人中预测正确的是:甲.
三人中预测正确的是:甲.
故答案为:甲.


科目:高中数学 来源: 题型:
【题目】若二次函数f(x)=4x2-2(t-2)x-2t2-t+1在区间[-1,1]内至少存在一个值m,使得f(m)>0,则实数t的取值范围( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解共享单车在![]() 市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了
市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了![]() 人进行分析,得到如下列联表(单位:人).
人进行分析,得到如下列联表(单位:人).
经常使用 | 偶尔使用或不使用 | 合计 | |
|
|
|
|
|
|
|
|
合计 |
|
|
|
(1)根据以上数据,能否在犯错误的概率不超过![]() 的前提下认为
的前提下认为![]() 市使用共享单车的情况与年龄有关;
市使用共享单车的情况与年龄有关;
(2)(i)现从所选取的![]() 岁以上的网友中,采用分层抽样的方法选取
岁以上的网友中,采用分层抽样的方法选取![]() 人,再从这
人,再从这![]() 人中随机选出
人中随机选出![]() 人赠送优惠券,求选出的
人赠送优惠券,求选出的![]() 人中至少有
人中至少有![]() 人经常使用共享单车的概率;
人经常使用共享单车的概率;
(ii)将频率视为概率,从![]() 市所有参与调查的网友中随机选取
市所有参与调查的网友中随机选取![]() 人赠送礼品,记其中经常使用共享单车的人数为
人赠送礼品,记其中经常使用共享单车的人数为![]() ,求
,求![]() 的数学期望和方差.
的数学期望和方差.
参考公式: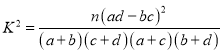 ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了积极支持雄安新区建设,某投资公司计划明年投资1000万元给雄安新区甲、乙两家科技企业,以支持其创新研发计划,经有关部门测算,若不受中美贸易战影响的话,每投入100万元资金,在甲企业可获利150万元,若遭受贸易战影响的话,则将损失50万元;同样的情况,在乙企业可获利100万元,否则将损失20万元,假设甲、乙两企业遭受贸易战影响的概率分别为0.6和0.5.
(1)若在甲、乙两企业分别投资500万元,求获利1250万元的概率;
(2)若在两企业的投资额相差不超过300万元,求该投资公司明年获利约在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|2≤x≤8},B={x|1<x<6},C={x|x>a},U=R.
(1)求A∪B,(CUA)∩B;
(2)若A∩C≠![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com