
【题目】下列结论错误的是 ( )
A. 命题“若![]() ,则
,则![]() ”的逆否命题为“若
”的逆否命题为“若![]() ,则
,则![]() ”
”
B. 命题“![]() ”的否定是
”的否定是 ![]()
C. 命题“若![]() ,则
,则![]() ”的逆命题为真命题
”的逆命题为真命题
D. 命题“若![]() ,则
,则![]() 且
且![]() ”的否命题是“若
”的否命题是“若![]() ,则m≠0或n≠0”
,则m≠0或n≠0”
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了如图所示的折线图.

根据该折线图,下列结论错误的是( )
A. 月接待游客量逐月增加
B. 年接待游客量逐年增加
C. 各年的月接待游客量高峰期大致在7,8月
D. 各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】唐三彩,中国古代陶瓷烧制工艺的珍品,它吸取了中国国画、雕塑等工艺美术的特点,在中国文化中占有重要的历史地位,在陶瓷史上留下了浓墨重彩的一笔.唐三彩的生产至今已有1300多年的历史,制作工艺十分复杂,它的制作过程必须先后经过两次烧制,当第一次烧制合格后方可进入第二次烧制,两次烧制过程相互独立。某陶瓷厂准备仿制甲、乙、丙三件不同的唐三彩工艺品,根据该厂全面治污后的技术水平,经过第一次烧制后,甲、乙、丙三件工艺品合格的概率依次为![]() ,
, ![]() ,
, ![]() ,经过第二次烧制后,甲、乙、丙三件工艺品合格的概率依次为
,经过第二次烧制后,甲、乙、丙三件工艺品合格的概率依次为![]() ,
, ![]() ,
, ![]() .
.
(1)求第一次烧制后甲、乙、丙三件中恰有一件工艺品合格的概率;
(2)经过前后两次烧制后,甲、乙、丙三件工艺品成为合格工艺品的件数为![]() ,求随机变量
,求随机变量![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
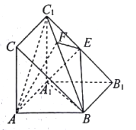
【题目】如图,直三棱柱ABC—A1B1C1中,侧面AA1B1B是正方形,AC丄侧面AA1B1B,AC=AB,点E是B1C1的中点.
(Ⅰ)求证:C1A∥平面EBA1;
(Ⅱ)若EF丄BC1,垂足为F,求二面角B—AF—A1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组 | 频数 | 频率 |
[10,15) | 10 | 0.25 |
[15,20) | 25 | n |
[20,25) | m | p |
[25,30) | 2 | 0.05 |
合计 | M | 1 |

(1)求出表中M,p及图中a的值;
(2)若该校高一学生有360人,试估计该校高一学生参加社区服务的次数在区间[15,20)内的人数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,请列举出所有基本事件,并求至多1人参加社区服务次数在区间[20,25)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,
,![]() ,
,![]() 为椭圆的两个焦点,
为椭圆的两个焦点,![]() 为椭圆上任意一点,且
为椭圆上任意一点,且![]() ,
,![]() 构成等差数列,过椭圆焦点垂直于长轴的弦长为3.
构成等差数列,过椭圆焦点垂直于长轴的弦长为3.
(1)求椭圆![]() 的方程;
的方程;
(2)若存在以原点为圆心的圆,使该圆的任意一条切线与椭圆![]() 恒有两个交点
恒有两个交点![]() ,且
,且![]() ,求出该圆的方程.
,求出该圆的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com