
���� ���������������������ʾ��f��x���Ľ���ʽ��������ϸ��Ϻ����ĵ��������f��x���ĵ��������䣻
������x�ʣ�-$\frac{��}{3}$��$\frac{��}{6}$�������$2x-\frac{��}{6}$�ķ�Χ����һ����f��x����ֵ��
�����������f������=$sin��2��-\frac{��}{6}��$=0�Ħ���ȡֵ���ϣ���Ϧ��ķ�Χ��ýǦ���ֵ��
��� �⣺������$\overrightarrow{a}$=��$\sqrt{3}$sin����+��x����cos��x����$\overrightarrow{b}$=��sin��$\frac{3}{2}$��-��x����-cos��x������
f��x��=$\overrightarrow{a}$•$\overrightarrow{b}$=$\sqrt{3}$sin����+��x��•sin��$\frac{3}{2}$��-��x��-cos2��x
=$\sqrt{3}$sin��x•cos��x-cos2��x=$\frac{\sqrt{3}}{2}sin2��x-\frac{1}{2}cos2��x$$-\frac{1}{2}$=$sin��2��x-\frac{��}{6}��$$-\frac{1}{2}$��
��f��x������С������Ϊ�У���$\frac{2��}{2��}=��$������=1��
��$f��x��=sin��2x-\frac{��}{6}��-\frac{1}{2}$��
��$-\frac{��}{2}+2k�С�2x-\frac{��}{6}��\frac{��}{2}+2k��$����ã�$-\frac{��}{6}+k�С�x��\frac{��}{3}+k�У�k��Z$��
��f��x���ĵ���������Ϊ[$-\frac{��}{6}+k�У�\frac{��}{3}+k��$]��k��Z��
����x�ʣ�-$\frac{��}{3}$��$\frac{��}{6}$��ʱ��$2x-\frac{��}{6}�ʣ�-\frac{5��}{6}��\frac{��}{6}��$��������ֵ��Ϊ[$-\frac{3}{2}��0$����
������f������=$sin��2��-\frac{��}{6}��$=0����$2��-\frac{��}{6}=k��$��
��$��=\frac{��}{12}+\frac{k��}{2}��k��Z$����0��������
��ȡk=0��1ʱ�����$��=\frac{��}{12}$��$\frac{7��}{12}$��
���� ���⿼��ƽ���������������㣬���������Ǻ����еĺ�ȱ任Ӧ�ã��������Ǻ�����ͼ������ʣ����е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{2}{5}$ | B�� | $\frac{1}{5}$ | C�� | $\frac{3}{10}$ | D�� | $\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��12��14��10�� | B�� | ��10��12��14�� | C�� | ��14��12��10�� | D�� | ��4��3��2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
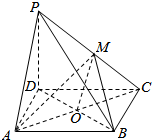 ��ͼ����֪PΪƽ���ı���ABCD����ƽ����һ�㣬M���߶�PC���е㣮
��ͼ����֪PΪƽ���ı���ABCD����ƽ����һ�㣬M���߶�PC���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1��3�� | B�� | ��3��-1�� | C�� | ��1��-3�� | D�� | ��-1��3�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com