
【题目】已知函数f(x)=x2+bx为偶函数,数列{an}满足an+1=2f(an-1)+1,且a1=3,an>1.
(1)设bn=log2(an-1),证明:数列{bn+1}为等比数列;
(2)设cn=nbn,求数列{cn}的前n项和Sn.
【答案】见解析
【解析】
(1)证明:∵函数f(x)=x2+bx为偶函数,
∴b=0,
∴f(x)=x2,
∴an+1=2(an-1)2+1,
∴an+1-1=2(an-1)2,
∴![]() =
=![]() =
=![]() =2.
=2.
∵a1=3,
∴b1=log22=1,
∴bn+1=2n.
即bn=2n-1,
∴数列{bn+1}是以2为首项,以2为公比的等比数列.
(2)解:由题意得cn=n2n-n.
设An=1×2+2×22+3×23+…+n×2n,
设Bn=1+2+3+4+…+n=![]() ,
,
∴2An=1×22+2×23+3×24+…+n×2n+1.
∴-An=2+22+23+…+2n-n×2n+1=![]() -n×2n+1=2n+1-n×2n+1-2,
-n×2n+1=2n+1-n×2n+1-2,
∴An=(n-1)2n+1+2.
∴Sn=An-Bn=(n-1)2n+1+2-![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ),将
),将![]() 的图象向左平移
的图象向左平移![]() 个单位长度后得到
个单位长度后得到![]() 的图象,且
的图象,且![]() 在区间
在区间![]() 内的最大值为
内的最大值为![]() .
.
(1)求实数![]() 的值;
的值;
(2)在![]() 中,内角
中,内角![]() ,
, ![]() ,
, ![]() 的对边分别是
的对边分别是![]() ,
, ![]() ,
, ![]() ,若
,若![]() ,且
,且![]() ,求
,求![]() 的周长
的周长![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业接到生产3000台某产品的A,B,C三种部件的订单,每台产品需要这三种部件的数量分别为2,2,1(单位:件).已知每个工人每天可生产A部件6件,或B部件3件,或C部件2件.该企业计划安排200名工人分成三组分别生产这三种部件,生产B部件的人数与生产A部件的人数成正比,比例系数为k(k为正整数).
(1)设生产A部件的人数为x,分别写出完成A,B,C三种部件生产需要的时间;
(2)假设这三种部件的生产同时开工,试确定正整数k的值,使完成订单任务的时间最短,并给出时间最短时具体的人数分组方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一鲜花店一个月(30天)某种鲜花的日销售量与销售天数统计如下:
日销售量(枝) | 0~49 | 50~99 | 100~149 | 150~199 | 200~250 |
销售天数(天) | 3天 | 3天 | 15天 | 6天 | 3天 |
将日销售量落入各组区间的频率视为概率.
(1)试求这30天中日销售量低于100枝的概率;
(2)若此花店在日销售量低于100枝的6天中选择2天作促销活动,求这2天的日销售量都低于50枝的概率(不需要枚举基本事件).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:
①分类变量![]() 与
与![]() 的随机变量
的随机变量![]() 越大,说明“
越大,说明“![]() 与
与![]() 有关系”的可信度越大.
有关系”的可信度越大.
②以模型![]() 去拟合一组数据时,为了求出回归方程,设
去拟合一组数据时,为了求出回归方程,设![]() ,将其变换后得到线性方程
,将其变换后得到线性方程![]() ,则
,则![]() 的值分别是
的值分别是![]() 和0.3.
和0.3.
③根据具有线性相关关系的两个变量的统计数据所得的回归直线方程为![]() 中,
中, ![]() ,
,
则![]() .正确的个数是( )
.正确的个数是( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在棱长均相等的正三棱柱ABCA1B1C1中,D为BB1的中点,F在AC1上,且DF⊥AC1,则下述结论:
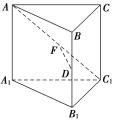
①AC1⊥BC;
②AF=FC1;
③平面DAC1⊥平面ACC1A1,其中正确的个数为( )
A.0 B.1
C.2 D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com