练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，P－ABCD是正四棱锥，ABCD－A1B1C1D1是正方体，其中

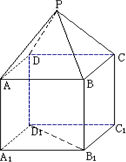
    (1)求证：PA⊥B1D1；

    (2)求平面PAD与平面BDD1B1所成的锐二面角的余弦值；

    (3)求B1到平面PAD的距离

    答案：
    解析：

    　　解：以为轴，为轴，为轴建立空间直角坐标系

    　　(1)证明：设E是BD的中点，P－ABCD是正四棱锥，∴

    　　又，∴　∴∴

    　　∴，即．

    　　(2)解：设平面PAD的法向量是，

    　　

    　　∴　取得，又平面的法向量是

    　　∴，∴．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2007年湖南省祁阳四中高三理科数学模拟试题 题型：044

    如图，P－ABCD是正四棱锥，ABCD－A1B1C1D是正方体，其中AB＝2，．

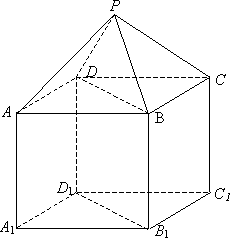
    (Ⅰ)求证：PA⊥B1D1；

    (Ⅱ)求平面PAD与平面BDD1B1所成的

    锐二面角的大小；

    (Ⅲ)求B1到平面PAD的距离．

    查看答案和解析>>

    科目：高中数学 来源：西安中学2007年高考理科数学模拟试题 题型：044

    如图，P－ABCD是正四棱锥，ABCD－A1B1C1D1是正方体，

    其中AB＝2，PA＝．

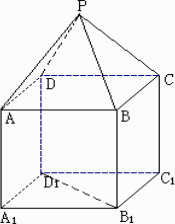
    (1)求证：PA⊥B1D1；

    (2)求平面PAD与平面BDD1B1所成的锐二面角θ的大小；

    (3)求B1到平面PAD的距离．

    查看答案和解析>>

    科目：高中数学 来源：山东济宁邹城二中2011-2012学年高二上学期期中质检数学理科试题 题型：044

    如图，P－ABCD是正四棱锥，ABCD－A1B1C1D1是正方体，其中

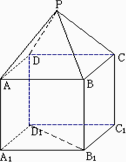
    (1)求证：PA⊥B1D1；

    (2)求平面PAD与平面BDD1B1所成的锐二面角的余弦值；

    (3)求B1到平面PAD的距离

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，P﹣ABCD是正四棱锥，，AB=2．

    （1）求证：平面PAC⊥平面PBD；

    （2）求该四棱锥的体积．

    查看答案和解析>>

    同步练习册答案